

In order to prove that the ratios of the perimeters equals 2, we will start with the GSP sketch from the previous page.
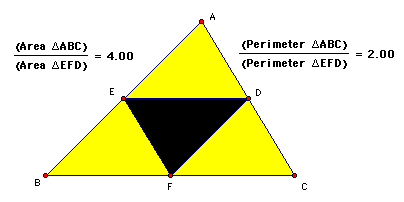
Here, we are given the triangle ABC with midpoints D, E, and F. For the purposes of this write-up that AB = segment AB.
First, find the perimeter of triangle ABC which equals AB + BC + AC and triangle DEF which equals DE + EF + DF. Since E, F, and D are midpoints, the segments connecting them are midsegments of the triangle ABC. The midsegment of a triangle parallel to the side of the triangle that it does not intersect and is half as long as that side. This gives the following: EF = .5AC, DF = .5AB, and ED = .5BC. These can now be substituted into the expression for the perimter of triangle DEF making the perimeter .5AC + .5AB + .5BC or .5(AC + AB + BC). Now that both expressions are in the same terms, it is time to find the ratio of the perimeters. So, the perimeter of triangle ABC divided by the perimeter of triangle DEF equals AC + AB + BC divided by .5(AC + AB + BC). Notice that there is an AC + AB + BC that can be cancelled. This leaves the ratio of the perimeters equal to 1 divided by .5 which equals 2.