

Assignment: Find two linear functions such that their product h(x) = f(x)*g(x) is tangent to each of f(x) and g(x) at two distinct points.
Let's simply start with two arbitrarily created
linear functions:
f(x) = 2x+2
g(x) = 4x+1
Using Graphing Calculator, we see that these lines appear as:
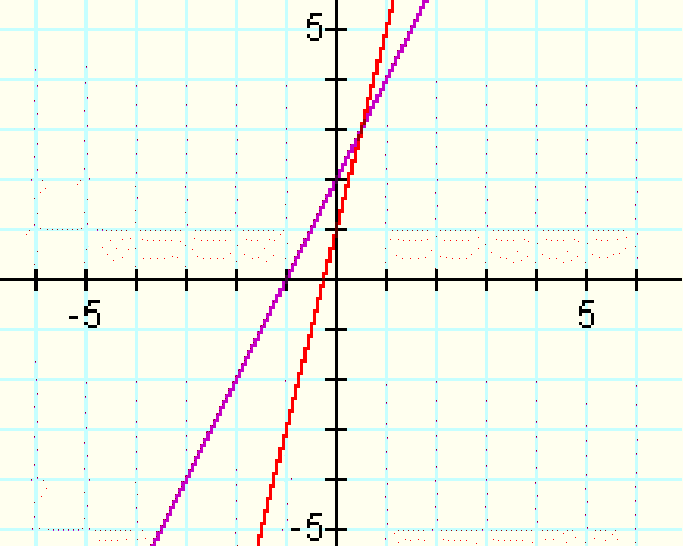
Since we need to find two linear functions that will be tangent to the graph of a quadratic function, which will be a parabola, it is obvious from the graph above that we need to change one of the equations so that the slope is negative. For the following graph, the slope on g(x) is changed to -4:
f(x) = 2x+2
g(x) = -4x+1
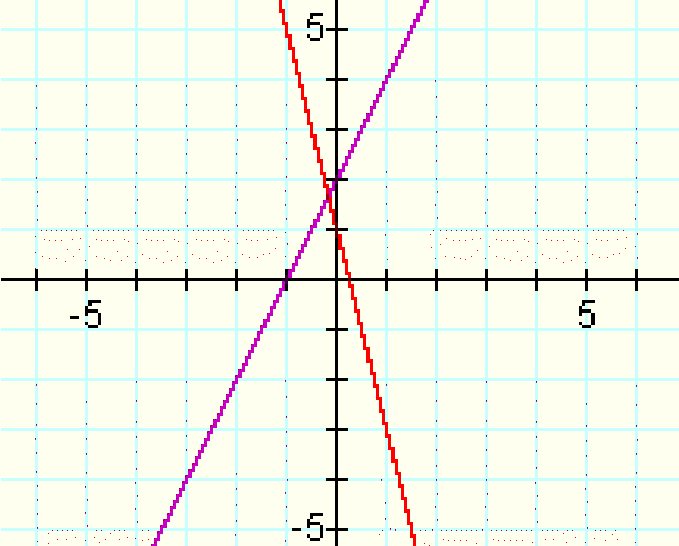
Now, let's add the product of these functions to the graph to see how close the parabola comes to tangency with either (or both) lines:
f(x)*g(x) = (2x+2)(-4x+1)
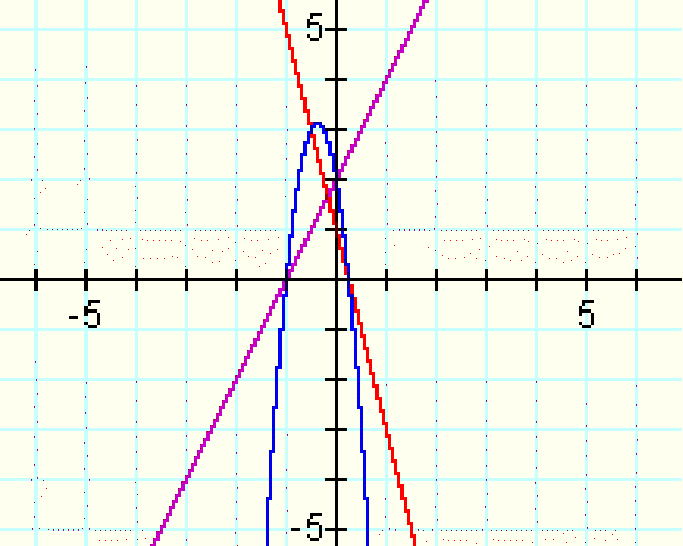
Clearly the product is not tangent to either line. Is it possible to manipulate the number so that the parabola, or product of the lines, will move down and the lines will move up?
Let's change the intercept of f(x) so that it will be lower on the y-axis.
f(x) = 2x+1
g(x) = -4x+1
Graph with the updated f(x) and the updated parabola:
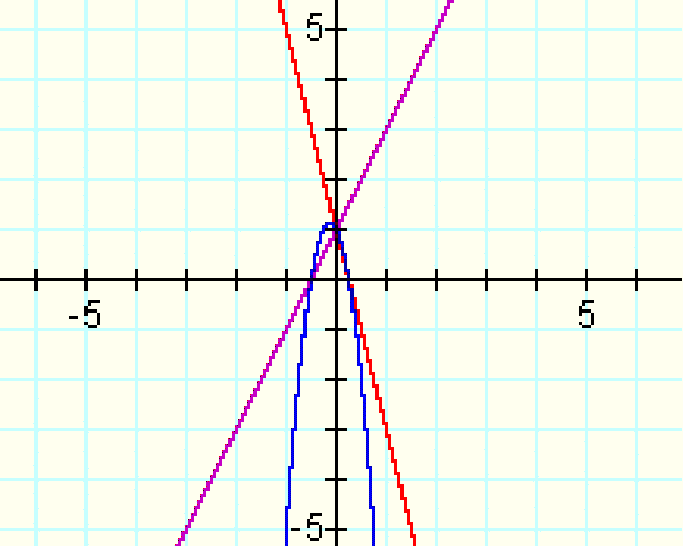
These are also not tangent, but are closer to tangency than the previous functions were.
To avoid spending too much time guessing at the changes, let's examine the mathematics behind tangency, and the conditions necessary so that a line is tangent to a curve.
What would be necessary conditions for the linear functions to be tangent to their product?
By definition, the slope of a line would need to be equal to the slope of the derivative of the curve (here, the product function) when evaluated at some point in order to be tangent at that point.
Since we are aiming to create a product function tangent to both linear functions that are its factors, we should use the same magnitude slope for each linear function to make it an easier fit to both lines.
Additionally, if we hope to have a parabola that is tangent to the linear functions at the x-axis, then we would be interested in finding points such that the parabola interesects the x-axis at the same value as the linear functions. In this case, we can look for a set of functions keeping in mind that the product function is equal to zero when either factor function equals zero.
Let's try setting the slopes equal to 1 and -1 so that they are the same and the product function equals both at some point:
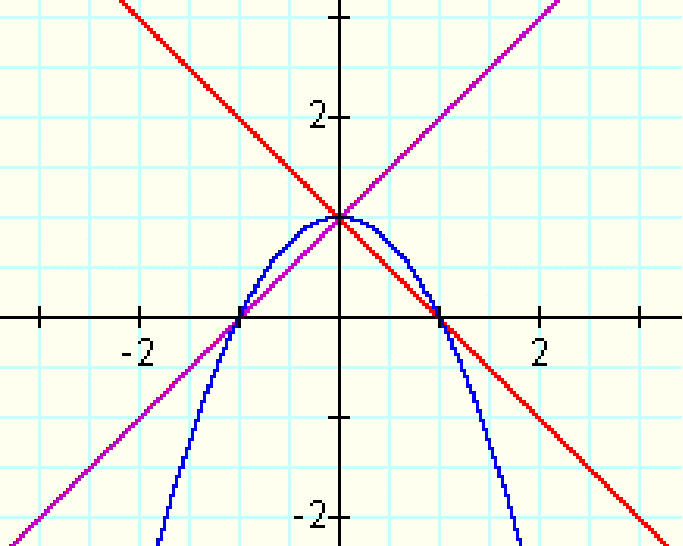
We see at points (1,0) and (-1,0) that the values are the same, but the parabola is still not tangent. Since the product parabola is above the lines, let's look at the slopes to see what would need to be changed so that the lines are above the parabola and not intersecting with the curve. The parabola needs to shift downward; how can we do this to the product without shifting the lines down? By using decimal values:
f(x)=x+.8
g(x)=-x+.8
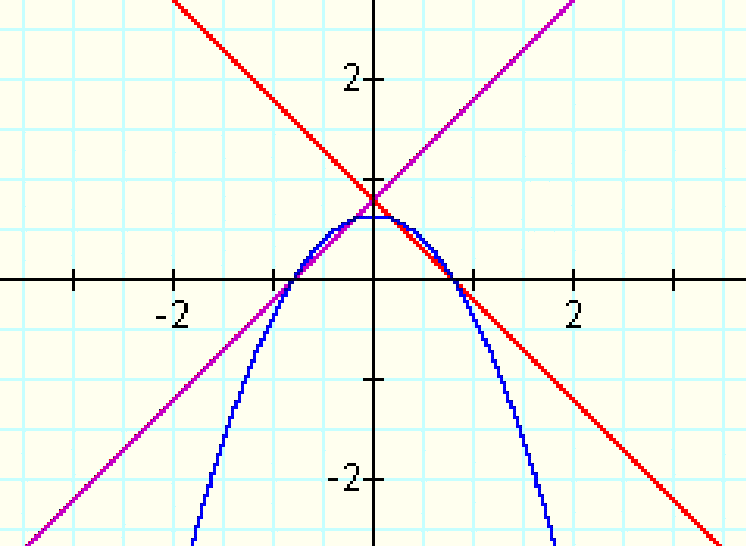
This is much closer. And if we try
f(x)=x+.6
g(x)=-x+.6
Even closer, but a zoom-in shot of one side of the graph shows us the lines are still not tangent:
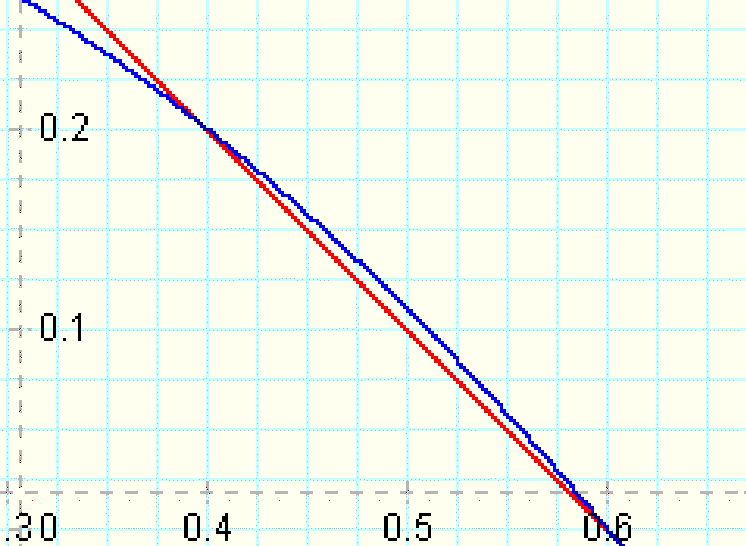
Let's try
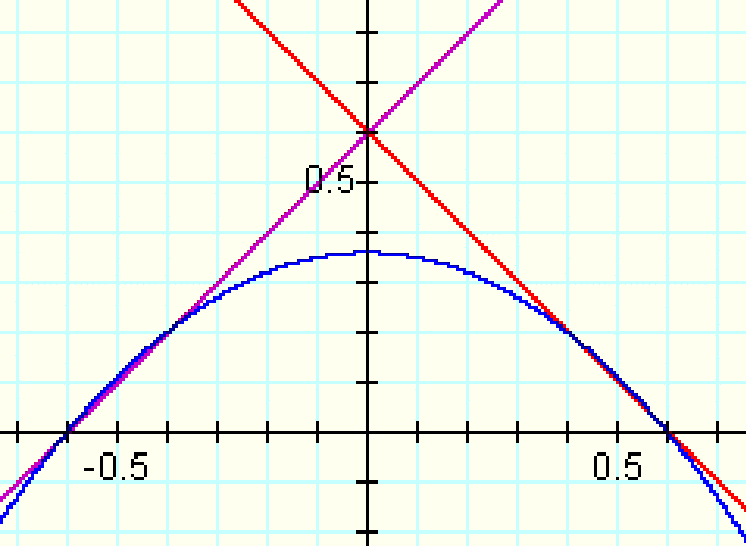
f(x)=x+.5
g(x)=-x+.5:
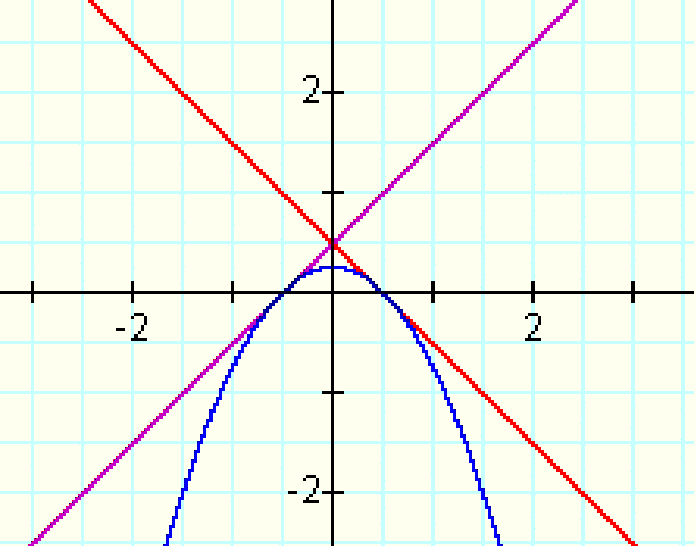
And zoom in for inspection:
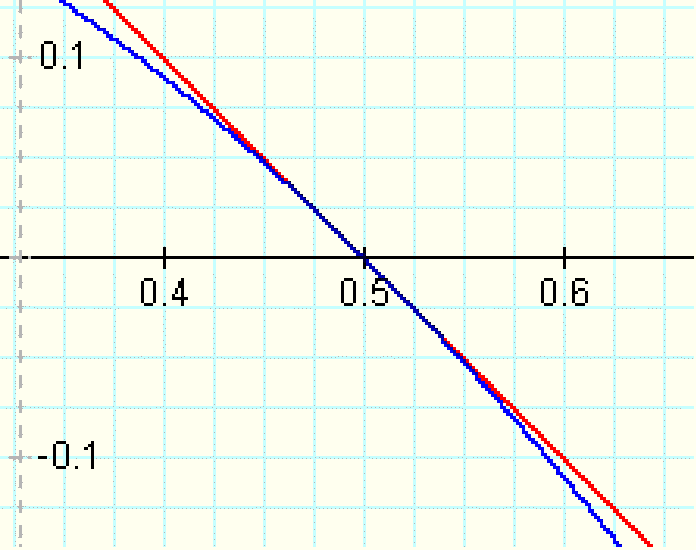
This appears to fit the criteria, so let's examine the functions more closely:
(-x+.5)(x+.5) = -x^2+x+.25
At x=.5 and x=-.5, the parabola interesects the x-axis.
From this we know that f(-.5) = 0, g(.5) = 0 and h(-.5), h(.5)=0
How can we be certain that there is a tangency and not an intersection? If we did not have the option of 'zooming in' at the tangency, how could we confirm mathematically that the curve is tangent to the line and does not intersect it? If the curve is tangent to either line at that point, the slope of the derivative of the product function will be equal to the slope of the linear function when evaluated at that point.
The derivative of the quadratic function is: -2x+1
At .5 and -.5, it's slope (-2x) becomes -1 and 1, respectively. As we see above, our linear functions have the slopes -1 and 1.
In general, when trying to find a quadratic function h(x) = f(x)*g(x), where g and f are linear functions...
It must be true that h(x0)=f(x0) and that h(x1)=g(x1) for some x0 and x1 in the domain of f,g,h.
It must also be true that the slopes of h'(xo) and h'(x1) equal the slopes of g and f at the respective points.