

Polar equations are equations that, instead of the cartesian coordinates x,y, use the measures r, theta where r=distance from the origin and theta = the measurement of the angle from the horizontal axis to the location of the point.
One well-known polar equation is the equation in the form:
r = a + b cos (kt)
When a and b are equal, this creates the 'k-leaf rose'. When k=1, we see the following graph:

When we set a=b (=1) and use different even
integer values for k that range from 2-12 ,
we can produce the following graph:
,
we can produce the following graph:
We have created a flower where k=the number of petals on the flower.
What can we expect to see if we remove the a-term from the equation? Below is a picture of the graphs with k ranging from 2 to 12 and a=0:
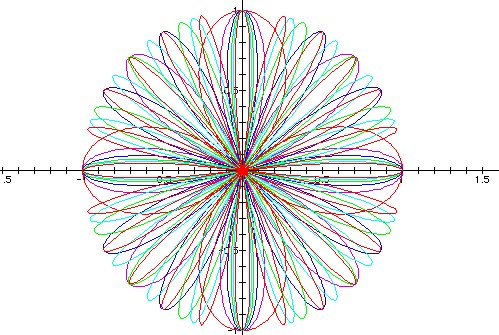 We see that mainly
the graph is reduced in size. Above the picture ranged from -2
to 2 along the vertical axis, here it is limited to the range
of the cosine function and it extends only from -1 to 1.
We see that mainly
the graph is reduced in size. Above the picture ranged from -2
to 2 along the vertical axis, here it is limited to the range
of the cosine function and it extends only from -1 to 1.
From this observation, we could also expect that increasing a and b would increase the size of the graph.
for k=6, a=3, b=3 we create the following image:
and for k=6, a,b=5 we create this graph: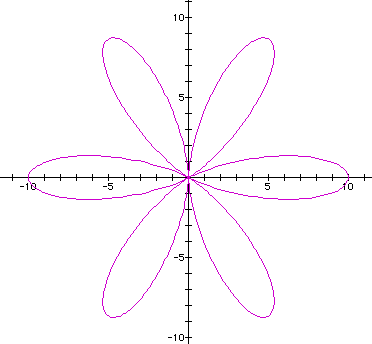
We can see from the increase in the range of values of the graph that increasing a and b does increase the size of the 'flower' by increasing the size of each 'petal'.
What could we expect if the cosine function is replaced with the sine function in these equations?

We can see that the shape is the same, but the graph is pointing into a different direction.
If we set a=b=1, and observe k at even integers in the interval 2-12:
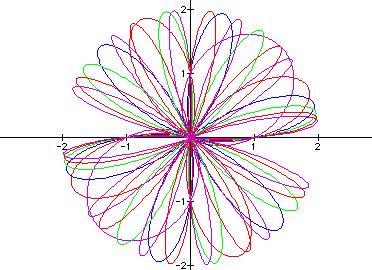
We see that the shapes of the equations are similar but in the sine function, there seems to be an area that is undefined. We can increase the value of k and see if this area remains undefined:
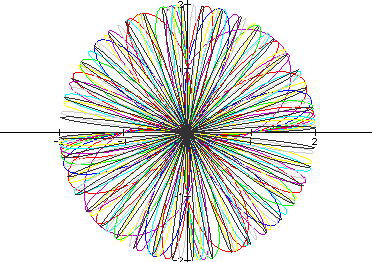 Here we have increased
k to 30 and we still see the smaller area just above and below
the horizontal axis where the graph is undefined.
Here we have increased
k to 30 and we still see the smaller area just above and below
the horizontal axis where the graph is undefined.
Let's remove the a term here and see just the sine function with the changing argument with k ranging from 2 to 10:

Without the added term a we can see the behavior of the sine function as it approaches the axes.
From these observations, we can see that polar equations can be useful not just for pretty pictures, but also to further our understanding of the sine and cosine functions.