

Using the midpoints of the sides of a triangle as vertices, we can create a medial triangle.
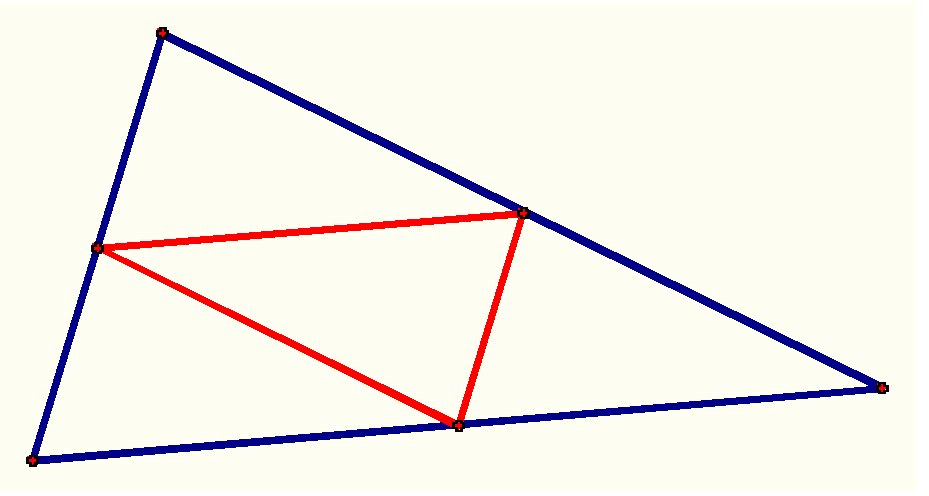
In this assignment, we are going to explore the centroid (G), orthocenter (H), circumcenter (C) and incenter (I) of the original triangle as well as these centers in the medial triangle.
The centroid (G) of a triangle is the
intersection of the three medians, which are the segments from
a vertex to the midpoint of the opposite side.
The centroids of the original triangle (G1) and the medial triangle
(G2) are shown here:
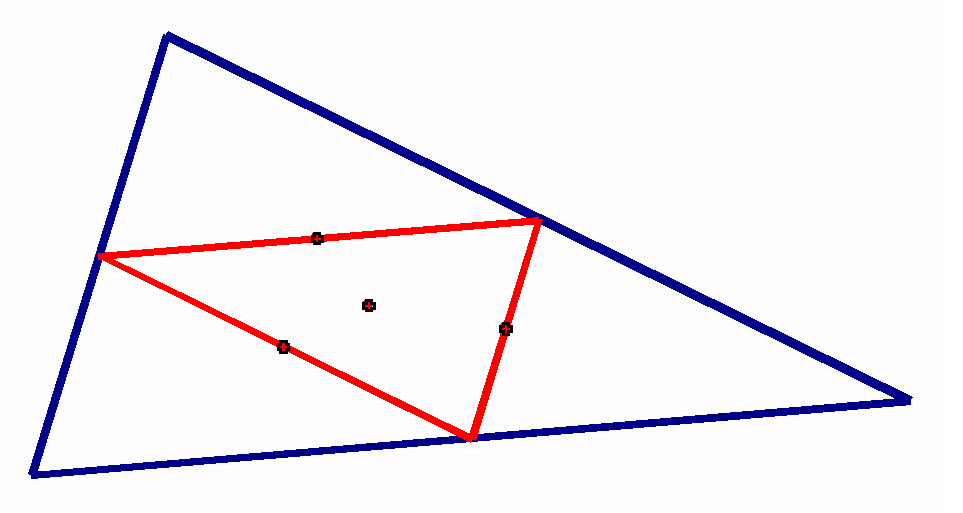
We see here that G1 and G2 are the same point. When we look at the medians used in the construction of the centroid, we can see that the centroid for the original triangle must be the same for the medial triangle. This is true because the vertices of the medial triangle are located at the side midpoints of the original triangle, and because the median segments of the original triangle pass through the midpoints of the sides of the medial triangle:
This is true regardless of the shape of the original triangle. To manipulate the shape of the original triangle and see that G1 and G2 remain at the same point, click here for a Geometer's Sketchpad sketch of the centroid.
The orthocenter of a triangle is the intersection of the three segments that contain the altitude of the triangle. An altitude is a perpendicular segment that connects a vertex of the triangle to the segment of the opposite side.
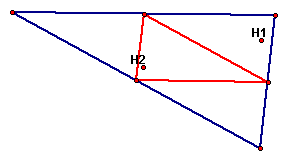
In this construction we see the orthocenters of the original triangle (H1) and the medial triangle (H2).
Unlike the centroids, the orthocenters of the triangles are different points. We see that if the medial triangle were a flipped mirror image of the original triangle, the orthocenter of the medial triangle is located similar to the original orthocenter.
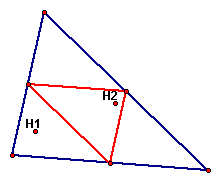
If the shape of the triangle changes,
we can see the shift in the locations of the orthocenter.
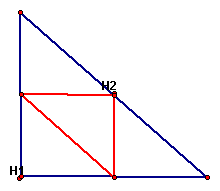
If we change the shape of the original triangle so that it is a right triangle,
the original orthocenter is located at the midpoint of the hypotenuse and the orthocenter of the medial triangle is located at the midpoint of its hypotenuse:
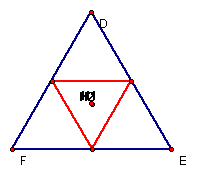
Additionally, if we change the shape of the original triangle so that it is an equilateral triangle, the orthocenter of the original triangle shares a location with the orthocenter of the medial triangle (which is also equilateral):
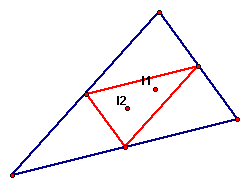
The Incenter of a triangle is the point on the interior of the triangle that is equidistant from the three sides of the triangle. A point on an angle bisector is equidistant from the sides of the angle; therefore, a point that is equidistant from all sides of a triangle would be located at the intersection of the angle bisectors.
Here we can see the incenter of the original triangle (I1) and of the medial triangle (I2):
If the original triangle is changed to an equilateral triangle, the incenters share the same point.
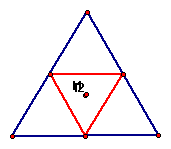
This can be shown to be true for any equilateral traingle and its medial triangle, because by definition, the incenter of the triangles is equidistant from all sides and on the angle bisectors. Since the original triangle is equilateral, the medial traiangle will be as well.
The circumcenter of a triangle is the point equidistant from the three vertices of the triangle. Since a point equidistant from two points on any side lies on the perpindicular bisector of the segment of that side, the circumcenter will be the point of intersection of the three perpindicular bisectors of the sides of the triangle.
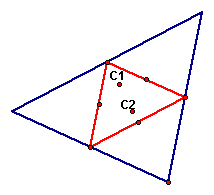
Additionally, the circumcenters are the center points of the circumcircle of the triangle, which is the circle that would include the vertices of the triangle:
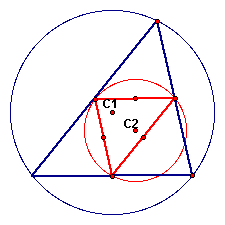
If the original triangle is altered to form a right triangle, the circumcenter of the original triangle is located at the midpoint of the triangle hypotenuse. The circumcenter of the medial triangle is located at the midpoint of its hypotenuse. The circumcircles formed are tangent at the right angle of the original triangle:
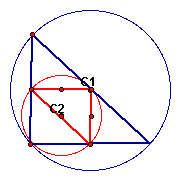
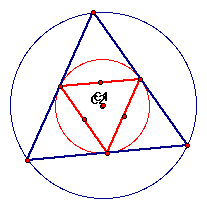
If the original triangle is changed to an equilateral triangle,
the circumcenters share a point:
Since we have seen that the centers of the medial and original triangles share locations in an equilateral triangle, what could we conjecture about the location of all centers in an equilateral triangle and its medial triangle?
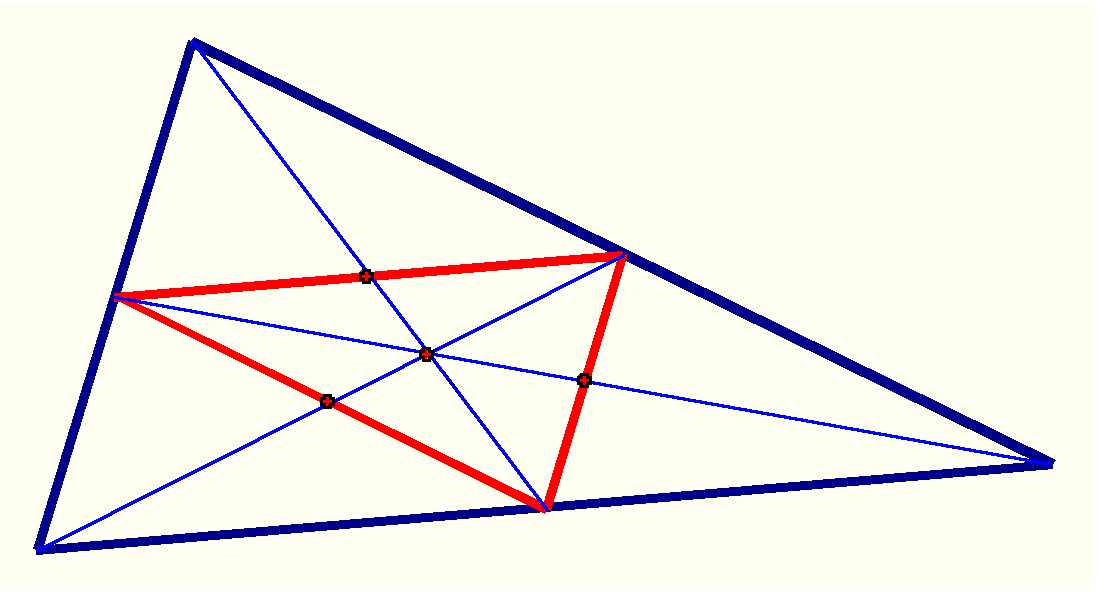
In this triangle and its medial triangle, the
centers of the triangle have been constructed: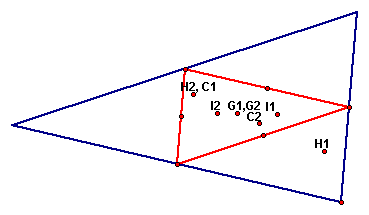
When we shift the original triangle to be an equilateral triangle, the centers align at the same point:
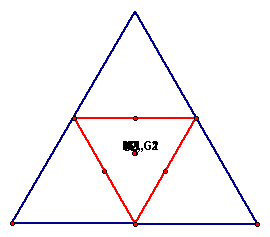
From this, we can conclude that when a triangle is equilateral, its medial triangle is equilateral, and the orthocenters, the circumcenters, the incenters and the centroids are the same point. This can be confirmed using the definition of each point:
Centroid: The centroid is the point at the intersection of the three medians. (A median is the segment from a vertex to the midpoint of the opposite side). We have already seen that the centroid in the original triangle is the same point as the centroid of its medial triangle. This is true for all triangles, including, of course, equilateral triangles.
Orthocenter: The orthocenter is at the intersection of the three altitudes (or of the lines containing the altitudes extending outside the triangle). An altitude is a perpindicular segment from a vertex to the opposite side. In an equilateral triangle, the base of each altitude is at the midpoint of each side. Therefore, in an equilateral triangle, the altitudes mimic medians and are segments from the vertices to the opposite midpoints. For this reason, the orthocenters of the medial and original triangles are at the same point as the centroids.
Circumcenter: The circumcenter is the point equidistant from the three vertices of the triangle. Since a point equidistant from two points lies on the perpindicular bisector of the segment joining the two points, the circumcenter is on the perpindicular bisector of each side of the triangle. In this equilateral triangle, the perpindicular bisectors will line up with the altitudes and the medians, and the intersection of the bisectors will be at the same point that the medians and altitudes intersect. For this reason, the circumcenters of the original and medial triangle are at the same point as the centroids and orthocenters.
Incenter: The
incenter is the point inside the triangle that is equidistant
from the three sides. Since a point equidistant from two sides
lies on the angle bisector, the incenter is at the intersection
of the three angle bisectors. In an equilateral triangle, the
angle bisectors will be lines that are perpindicular to the opposite
side and will intersect the opposite sides at their midpoints.
Because the bisectors create segments from each vertex to the
midpoint of the opposite side, they align with the medians, the
altitudes, etc. and the incenters of the original and medial triangles
are located at the same point as the other centers.