

A 4'x4' picture hands on a wall such that its bottom edge is 2 ft above your eye level. How far back from the picture should you stand, directly in front of the picture, in order to view the picture under the maximum angle?
Side View:
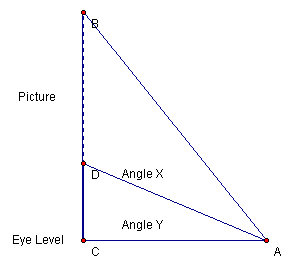
The maximum viewing angle would be that angle at which Angle Y in the above illustration is maximized. We need to find the optimal distance from point C that we should stand (point A) to maximize Angle X. Angle BAC = Angle X + Angle Y.
From the illustration, we can define the measures of Angle Y and Angle X as dependent on the distance from the picture to the viewer (CA).
In the triangle formed, we know that ACB is a right angle, it is the angle between the floor and the wall on which the picture is mounted (at least, we hope it is a right angle and will assume so for the rest of the calculation). Because of this, we can use trigonometric functions to find the measure of Angle BAC, Angle X and Angle Y for various distances from the painting (various measures of CA).
The tangent of Angle BAC (tan BAC) = 6/CA.
The tangent of Angle X (tan X) = 2/CA.
To find the measure of Angle Y from these, we will need to use the inverse tangent function:
tan-1 (Angle Y) = tan-1 (6/CA)- tan-1 (2/CA).
Since we are trying to find the maximum value for Y, we can take the derivative of the inverse tangent function with respect to CA and find the point at which the derivative is equal to zero.
dY/dCA = 1/(1+(36/CA2)(-6/CA2) 1/(1+(4/CA2)(-2/CA2)
Set equal to zero, to find the inflection point, and solve for CA to find the distance from the wall at the inflection point:
0 = (-6)/(CA2+36) + (2)/(CA2+4)
CA2 = 96/8
CA = (12)1/2
CA ~ 3.5
We know, then, that for a maximum viewing angle, we should stand 3.5 feet away from the picture on the wall.
Here is a link to a GSP file of this image. If you adjust the length of AC to change the viewer's position, do you see the same results?