

Below is a construction of triangle ABC; its Orthocenter, H; the orthocenter of triangles HCB, HAC, HAB and the circumcircles of triangles ABC, HBC, HAB and HAC.
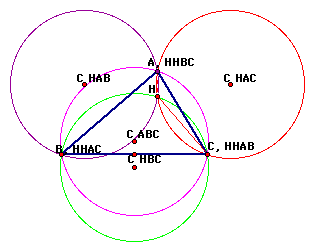
If the vertex A is moved to align with the Orthocenter of ABC, the picture looks like this:

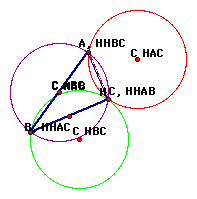
Similarly, if the vertex B of ABC is aligned with the Orthocenter H of ABC we see the following picture:
Conjecture: The Nine Point Circles for ABC, HBC, HAC and HAB will overlap entirely and show as only one circle:
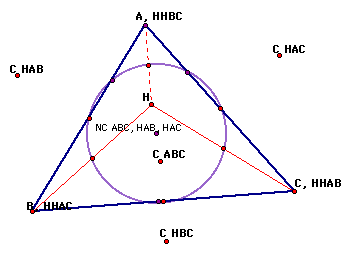
The Nine-Point Circles will be the same for these triangles if the nine points are identical for each triangle. Because the center for the circle is determined using the points of the circle, it is only necessary to show that the nine points of the circle are exactly the same to know that the circle for every triangle is identical.
This can be proven for any triangle ABC, its
Orthocenter H and the triangles HBC, HAC, and HAB: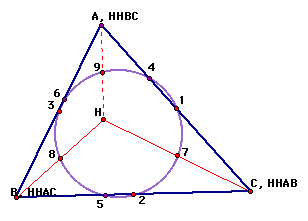
The nine points of a nine-point circle are:
the midpoints of the three sides of the triangle
(points 1,2,3),
the three points at the base of the three altitudes of the triangle
(points 4,5,6) and
the three midpoints of the segments drawn from the vertices
of the triangle to the orthocenter (points 7,8,9).
In triangle ABC, the points would be numbered as above.
In triangle HBC, the midpoints of the sides of the triangle would become: 7,8,2. The bases of the three altitudes would be 5,4,6. Because the altitude for HBC is located at point A, the midpoints of the segments drawn from the vertices (points H,B,C) would be 1,3 and 9. We can see from this collection that the points for the nine point circle of HBC include all of the original points 1-9. This is illustrated below including the lines of alitude:
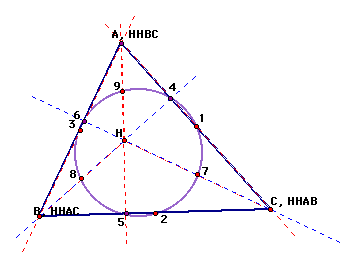 In this illustration,
the lines of altitude are red and the blue dotted lines are extensions
of the sides of HBC. From this it is easy to see that the orthocenter
is point A and that the altitudes intersect with the lines of
the sides of the triangle at points 4,5,6.
In this illustration,
the lines of altitude are red and the blue dotted lines are extensions
of the sides of HBC. From this it is easy to see that the orthocenter
is point A and that the altitudes intersect with the lines of
the sides of the triangle at points 4,5,6.
For triangle HAC, the midpoints of the sides are 1,7,9. The orthocenter is located at point B, so the midpoints from the vertices to B are located at points 2,3,8. The altitudes of triangle HAC intersect the sides at points 4,5,6. Again, the nine points listed above are included here as well.
Likewise, for triangle HAB, the altitudes intersect the lines created by the triangle sides at points 4,5,6. The orthocenter for triangle HAB is located at point C. Therefore, the midpoints of the segments connecting the orthocenter to the triangle's vertices are at points 1,2 and 7. And the midpoints of the sides of the triangle include points 3,8 and 9. We can conclude that the nine points are identical to those listed above and therefore the nine point circle will be identical.