 Let ABC be any
triangle. Then if P is any point in the plane, the triangle formed
by the segments created after constructing perpindiculars
to the sides of ABC and connecting their intersections is called
the Pedal Triangle.
Let ABC be any
triangle. Then if P is any point in the plane, the triangle formed
by the segments created after constructing perpindiculars
to the sides of ABC and connecting their intersections is called
the Pedal Triangle.
In this assignment, we will explore what happens to the pedal triangle (where is it located in relation to ABC? what is its shape?) when the pedal point (P) is located at varied 'key' locations with respect to triangle ABC.
If the pedal point is located at a vertex of ABC:
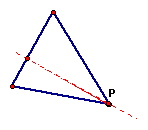 The pedal triangle
collapses into a line that connects a vertex with its opposite
side and is perpindicular to the opposite side. The line forms
an altitude of ABC.
The pedal triangle
collapses into a line that connects a vertex with its opposite
side and is perpindicular to the opposite side. The line forms
an altitude of ABC.
If the pedal point is located at the orthocenter of ABC:
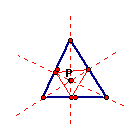 The
pedal triangle is located within ABC and lines up so that its
vertices are located at the bases of the altitudes contained in
ABC.
The
pedal triangle is located within ABC and lines up so that its
vertices are located at the bases of the altitudes contained in
ABC.
I
f the orthocenter is located outside ABC, then:
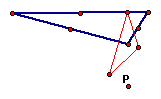 The pedal triangle
shifts so that some part of it is outside ABC; however, some portion
of the pedal triangle also remains inside ABC.
The pedal triangle
shifts so that some part of it is outside ABC; however, some portion
of the pedal triangle also remains inside ABC.
If the pedal point is located at the centroid of ABC:
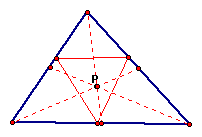 The pedal triangle
is located entirely in the interior of ABC.
The pedal triangle
is located entirely in the interior of ABC.
And if ABC is an equilateral triangle:
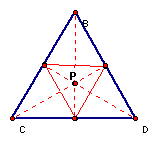 Then the pedal
triangle lines up so that its vertices are at the midpoints of
ABC.
Then the pedal
triangle lines up so that its vertices are at the midpoints of
ABC.
If the pedal point is located at the incenter of ABC:
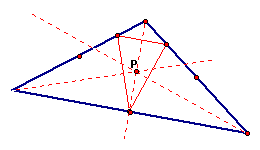 The
pedal triangle is located inside triangle ABC. Since we have shown
in assignment 4 that that all of the triangle's centers line up
at the same point in an equilateral triangle, we can conclude
that every time ABC is an equilateral triangle, the pedal triangle
will have its vertices at the midpoints of the sides of ABC, as
we have seen in the above example.
The
pedal triangle is located inside triangle ABC. Since we have shown
in assignment 4 that that all of the triangle's centers line up
at the same point in an equilateral triangle, we can conclude
that every time ABC is an equilateral triangle, the pedal triangle
will have its vertices at the midpoints of the sides of ABC, as
we have seen in the above example.
If the pedal point is located at the circumcenter of ABC:
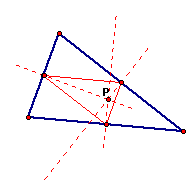 The
pedal triangle is located within ABC. Additionally, because the
pedal triangle's circumcircle shares a center point with the circumcircle
of ABC, the pedal circumcircle is always within the circumcircle
of ABC.
The
pedal triangle is located within ABC. Additionally, because the
pedal triangle's circumcircle shares a center point with the circumcircle
of ABC, the pedal circumcircle is always within the circumcircle
of ABC.
f the circumcenter is located outside ABC:
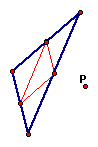 The
pedal triangle is still always located inside ABC. Click
here for a link
to a GSP file where you can manipulate the circumcenter and P
to see that this is always true.
The
pedal triangle is still always located inside ABC. Click
here for a link
to a GSP file where you can manipulate the circumcenter and P
to see that this is always true.
If the pedal point is on the side of the triangle:
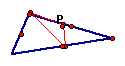 The
pedal triangle will be located inside or outside of ABC. It will
always be true that one of the vertices of the pedal triangle
will be at point P.
The
pedal triangle will be located inside or outside of ABC. It will
always be true that one of the vertices of the pedal triangle
will be at point P.
If the pedal point is located at the center of the nine point circle for triangle ABC:
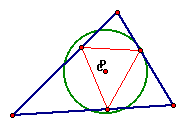 Then the pedal triangle will be located within the
nine point circle and within ABC. If the centerof the nine-point
circle is located outside of the triangle, then the pedal triangle
will be located within the circle but not within ABC:
Then the pedal triangle will be located within the
nine point circle and within ABC. If the centerof the nine-point
circle is located outside of the triangle, then the pedal triangle
will be located within the circle but not within ABC:
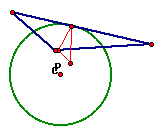
Since the pedal triangle is defined by the location of the pedal point and the perpindicular lines connecting the point to the triangle, it would be expected that selecting a location at one of the triangle's centers/sides/vertices would have some effect on the location of the pedal triangle. For each of these instances, it is possible to prove that the pedal triangle's location must be where it is, but here we will do only one proof.
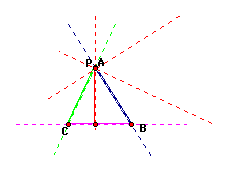
Given the triangle ABC, the pedal point P and the pedal triangle. If P is located at a vertex of ABC, A, then we will expect the pedal triangle to collapse into a line that forms an altitude of the triangle. Why can we expect this?
The pedal triangle is formed from the segments that join the intersections of the lines that are perpindicular connectors of P and the sides of the triangle. Here is an illustration of the pedal triangle that includes the lines used to find the intersections:
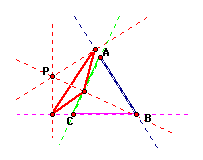 When we move P to
be at the vertex A, then we can see that its perpindicular connector
to the opposite side is the altitude of the triangle. Additionally,
the lines that are perpindicular between P and the adjoining sides
will intersect at point A. Therefore the segment creating the
triangle is only one line that connects vertex A to the base of
the altitude.
When we move P to
be at the vertex A, then we can see that its perpindicular connector
to the opposite side is the altitude of the triangle. Additionally,
the lines that are perpindicular between P and the adjoining sides
will intersect at point A. Therefore the segment creating the
triangle is only one line that connects vertex A to the base of
the altitude.