

This investigation is to begin to look at the polar equation:
where a, b, and k, are elements of the Rational Numbers. From past experienced with polar equations of this form one might remember a set of rules or names for different situations. It is the purpose of this write-up to connect these ideas into a family of curves for equations of this form. We will be looking at varying values of a,b, and k and try to acknowledge any relationships between these. Consider the equations when we let a = b = 1 and vary values of k in terms of the integers.:

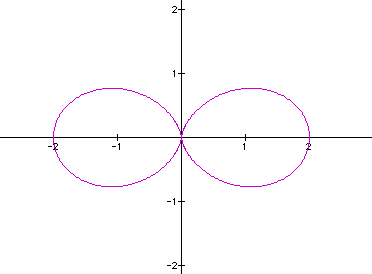
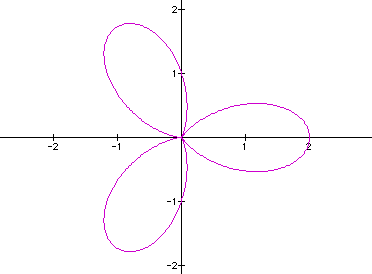
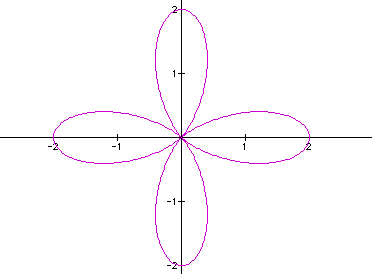
From looking at the k-leaf roses it appears as if the positive integer value of k describes and creates the number of pedals of the figure. It remains to be a constant between the four curves let's look at a larger value of k, say 20.
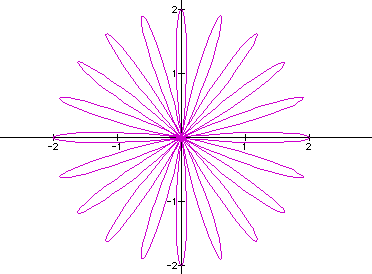
We see that this relationship also holds true as there are 20 pedals on this figures. Another relation that seems to be coming out is that the length of each pedal is 2. Does this correspond to a + b? Let's look at other where a = b. Consider the varying a = b and we will set k at 4.
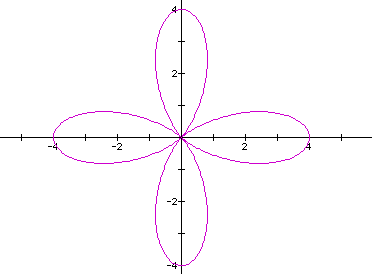
Upon looking at the equation we see that a + b = 4 which in fact is the length of each pedal. Looking at another possibility, a = b = 5/2. We should have a 4-leaf rose with each pedal having length of 5.
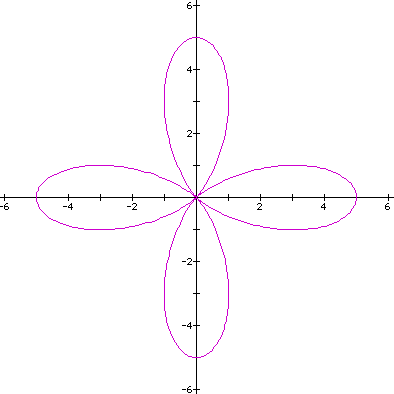
Which is the case. Notice that we have been looking at a = b. Let's consider a > b. Consider the equation when a = 3 and b = 2. From our look at a = b we might say that we could have the same curve as just shown but will we?
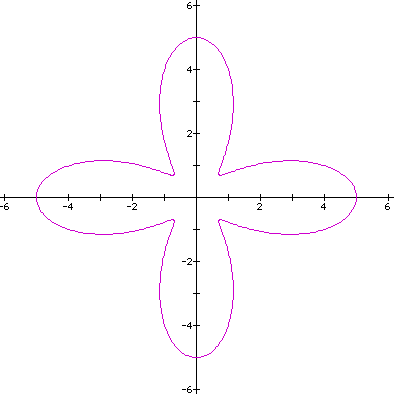
Looking at the similarities of the last two curves we see that when a = b = 5/2 and k = 4 we had a 4-leaf rose with pedal length of 5. Now when we let a = 3 and b = 2 with k remaining constant we see that the curve opens up. There is still 4 pedals. The length of each pedal is still 5 but the figure alters. Now let's look at a < b. Consider a = 2 and b = 3. What similarities and differences might you expect?
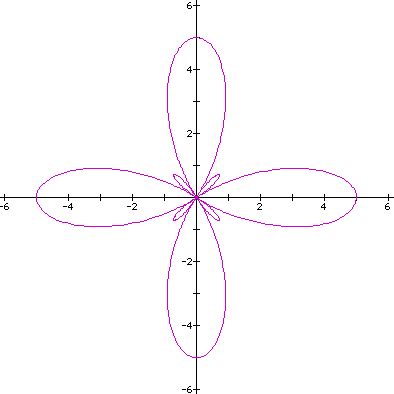
If we look at the similarities we still have the four major leafs with length of 5 but there are now four minor leafs. Let's look at another say a = 3 and b = 4.
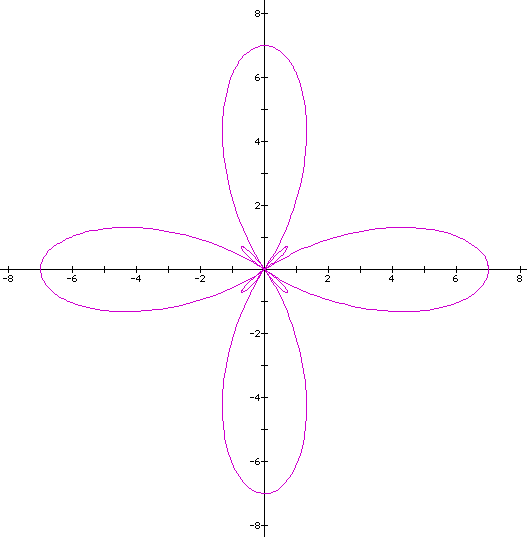
Our major leafs still hold true on our assumptions. The interesting thing is that the minor leafs seem to remain constant in size from the last two examples. Let's let a = .25 and b = .75. What should the figure look like?
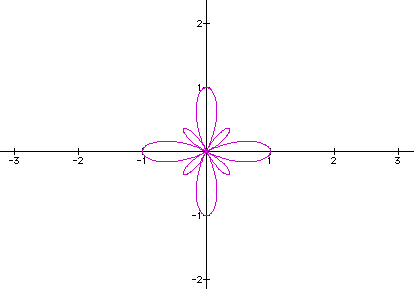
It seems as if the major leafs still play their role in our assumptions but in this case the minor leafs do shrink compared to our first two examples of a < b.
For all of these a < b we have let k remain constant at 4. Let's vary k a bit. Consider:
from our past graphs, a common thought should be 3 major leafs of length 3 and 3 minor leafs between the major leafs but with a odd value of k things are not exactly as expected, the graph:
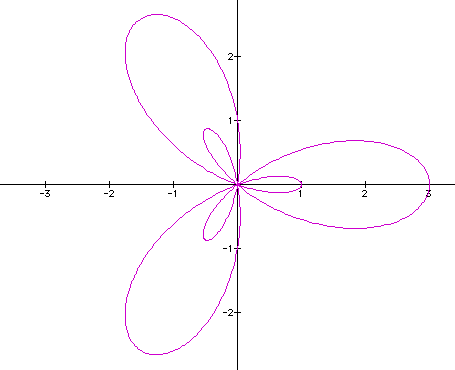
The major difference between k being an even integer and k an odd integer is that when k is odd the minor leafs appear in the interior of the major leafs. Another example:
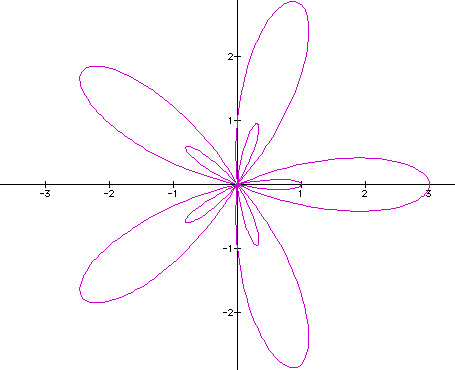
Just as when k = 3 we have a similar curve when k = 5. 5 major leaves of length 5 and 5 minor leafs embedded in the interior of the majors.
I) the length of the major pedals is a + b,
II) when a = b we will have a k-leaf rose
III) when a > b our k-leaf rose will expand from the origin to create a curve that opens,
IV) when a < b we have two case: Case I when k is an even integer we will have k major leafs of length a + b and k minor leafs between the major leafs. Case II when k is odd we still have k major leafs of length a + b but k minor leafs will be in the interior of the major leafs.
During this investigation we held k to the integers. Let's look when we let k be a rational number.
For this will focus on the polar equation of the form:
Since we have covered case when the parameter multiplying theta is an integer we can look at the two cases.
Case I: k > 1
Case II 0 < k < 1
Consider the equation:
This graph might be more difficult to predict due to how can we have 1.5 pedals. We should acknowledge that for all of these graphs we have let a = 0 and b = 2 therefore a length of 2 for some leaf might show up. Also since a does not equal b we should have some representation of minor leafs.
The Graph of this equation:
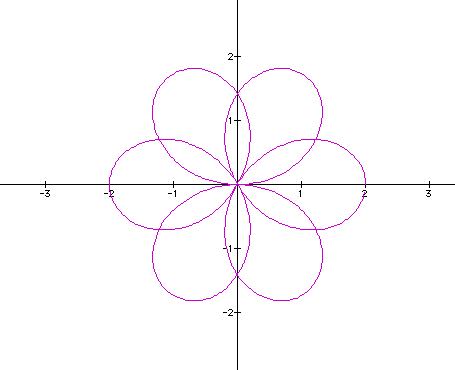
Looking at this curve we have 6 major leafs of length 2. Also we have six minor leafs whose endpoint is at the intersection of the major leafs. Another example:
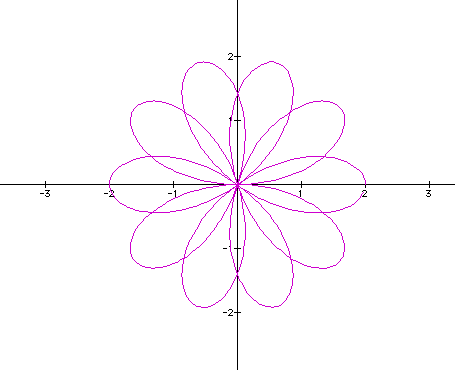
Upon inspection, we see ten major leafs of length 2 and ten minor leafs. From the last two n-leaf roses it seems as if there is a relationship between the number of leafs and the numerator and denominator of the rational number multiplying theta. That is the number of leafs is equal to the product of the numerator and the denominator. For example in the first rational k we had (3)(2)=6 and the the second example was (5)(2) = 10. Let's look at another.
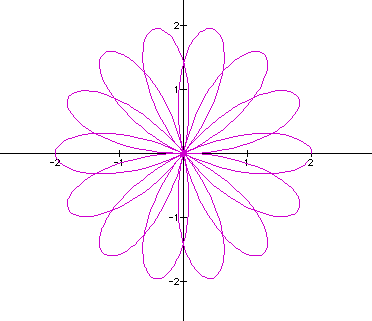
As we see our assumption holds true. Notice for all k of the form a / b where b did not divide evenly into a we looked at values such that a > b. Consider when a < b.
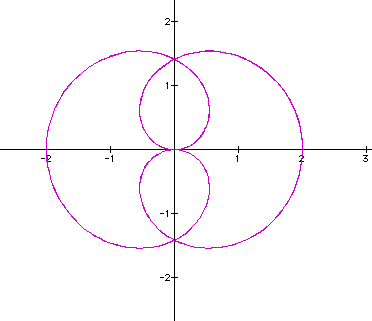
Notice that this not the same as when a > b but what we have is the union of two cardioids or 1-leaf roses. Let's try 2/3.
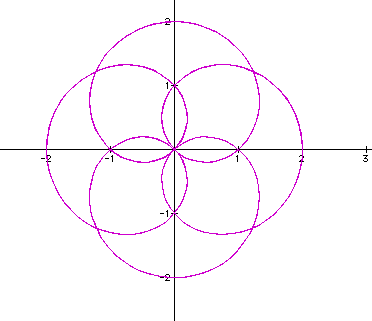
Yet another interesting curve which appears to be the union of four cardioids. There is a number of these that can be tried and analyzed.
The vast realm of these non-integer rational parameters on theta our endless. From looking at more examples one can lead themselves to other conjectures and proofs. Try looking at a > b when b = 4 or 6 or 8. I know you won't be disappointed.
BFM