This investigation is to examine the effect of real numbers a, b, and c on the curve of y =sinx. To begin we will look at each variable individually on the sine curve. When we finish looking individually at the variables we can easily show what happens to the sine curve when two or more of the parameters change.
To begin with let's take at a brief look at the basic sine curve:
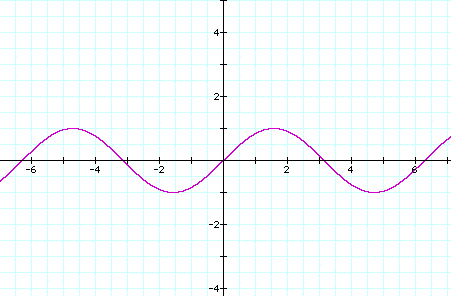
As you might have noticed from previous studies of the sine function the domain of sinx is all real numbers while the range is [-1,1].
Now that we have refreshed ourselves with the
sine curve let's take a look at what happens with various changes
in the parameter "a".
The amplitude of the sine function controls the range of the function. In Graph 1 the value of a was 1 (sinx = (1)sinx). Let's compare positive integers for "a".
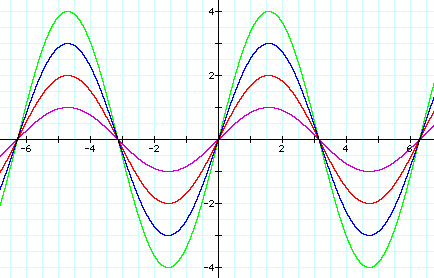
When we look at the four graphs on Graph 2 you should notice that the ranges of each sine function is [-a, a].
Now let's compare y = (1)sinx to sine curves with negative integers for a
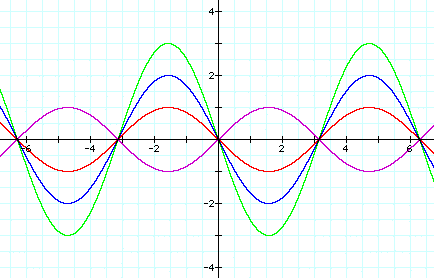
In Graph 3 let's look at the first two curves
(y = sinx
and y = (-1)sinx). You should notice that the range of both of these
functions is [-1, 1] but curves mirror each other. From the positive
values of "a" we said that the range was [-a, a] but
you should notice for negative values of a that the range is [a,
-a]. Therefore for this form of sine function, y = asin[b(x +
c)] we can conclude that the range is [
,
]
In conclusion about the parameter "a"
we can conclude that the value of a controls the distance above
and below the x-axis that the sine curve travels and stipulates
either exactly what the range is for the function or will be used
to calculate the range
Try
These I:
1. For the function y = 6sinx:
A. What is the range of this function?
B. Graph the function when x is in the interval [-6, 6].
2. For the function y = -7sinx
A. What is the range of this function?
B. Graph the function when x is the interval [-6, 6].
For this next section let's let a=1 and c=0. Now let's compare y=sinx to y=sin(bx) for a couple of values of b
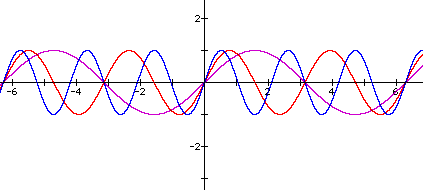
Visually, it is not as easy to see what happens
when we change values of "b" but from your previous
work with sine you should remember that the period is 
. Therefore
when b = 1 (y = sin (1x) ) the period is
.
If you notice when we change the values of b the period of the
each function changes. In fact, as "b" increases the
period of the function actually decreases.
By Rule: period of sine function = 
.
So if we notice for y = sin(2x), b=2, the period
= 
= 
. (Approx
3.142).
So the Graph does one full period during a
distance on the x-axis of 
.
Now that we have looked at positive values
of "b" it would make sense to look at negative values
of "b" but this is not that exciting since sin(-x) =
-sinx. Therefore if we were to look at y = sin(-2x) that should
be the same as y = -sin(2x). Which tells me that a = -1 and b
= 2. From the amplitude section a negative value for "a"
tells us that the graph is a mirror image of the positive values
and when b = 2 that tells us that the period is 
.
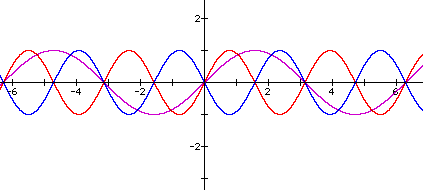
Notice that y = sin(2x) and y = sin(-2x) are "mirror" images of each other and notice that their respective periods are the same.
Try These II:
1. y = sin(4x)
A. What is the range of this function? What is the period of this function?
B. Graph this function over [0, 3.142]
2.
A. What is the range of this function? What is the period of this function?
B. Graph this function over
[0, 
].
3. y = 6sin(2x)
A. What is the range of this function? What is the period of this function?
B. Graph this function over
[0, ].
For our investigation into what happens when we change values of "c" we will use the values of a = 1 and b = 1 for our initial look. The term "phase shift" means an actual shift of the y-axis. To see this lets look at a few examples:
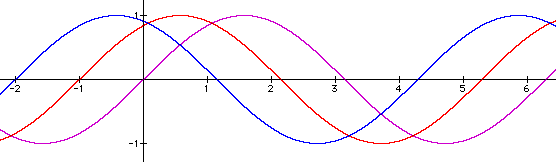
If we look at these changes in "c" we can see for y = sinx, c = 0 therefore the y-axis remains the same but when we look at y = sin(x + 1) and y = sin(x + 2) the values of "c" are 1 and 2 respectively. Notice that a value of c = 1 meant a translation of the y-axis 1 unit to the left and a value of c = 2 meant a translation of the y-axis two units to the left. If you look at the three different graphs you will see that there is neither a change in range for each function nor is there a change in period.
It seems as if any positive value of "c" means the sine curve will shift "c" units to the left. On the other hand it would make intuitive sense that a negative value for c would mean a shift of c units to the right for all points on the curve. Let's investigate:
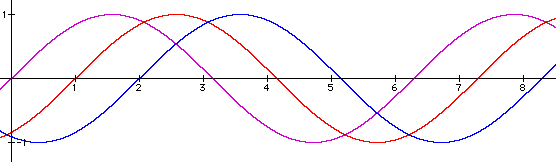
Upon investigation we see that is actually the case. We can conclude the the value of c has a "movement" feature to the sine curve.
Try These III:
1. y = sin(x + 3)
A. What is the range, period, and phase shift for this function?
B. Graph this function.
2. y = 5sin(x - 3)
A. What is the range, period, and phase shift for this function?
B. Graph this function.
Summarizing the three parameters we can conclude the following:
I. For change in "a" - The parameter "a" controls the range of this type of function. It also controls the maximum and minimum for the function.
II. For change in "b" - The parameter "b" controls the period of the function.
III. For change in "c" - The parameter "c" controls the translation of the y-axis and all points on the curve.
With this knowledge the only "graph" you need to know is that of the base sine curve and then what each parameter does and you can graph any function of the form:
So let's look at a example:
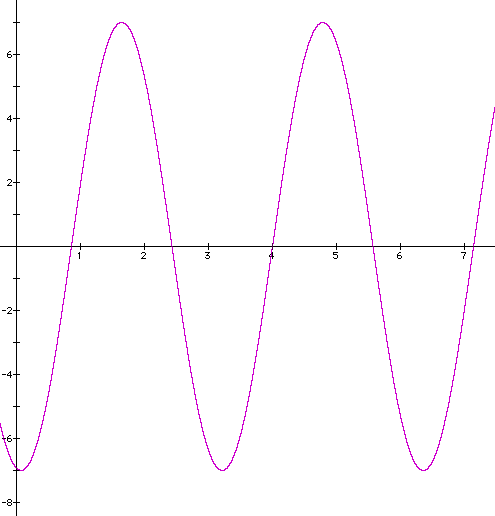
Graph y = 7sin2(x - 4) showing at least two full periods.
a = 7: range is [-7, 7]
b = 2: period is 
= 
(Approx = 3.142)
c = -4: y-axis is shifted 4 units to the right.
The graph would have one full period between x = [4, 4 + 
] and another [4 - 
,
4]
So the graph should look like this:
Try These IV:
1. For the function: y = 3sin[0.25(x + 2)]
A. What is the range, period, and phase shift for this function?
B. Graph at least two full periods of this function.
2. For the function y = 2sin[6(x - 1)]
A. What is the range, period, and phase shift for this function?
B. Graph at least two full periods of this function.
I hope that this write-up has been helpful to you the student/reader. If there are any questions or problems with any type of sine function of this form please send me a comment at my email on my home page. Have a good one.
BFM
Return to Brock F. Miller's Page