---

In this investigation we will be looking at various quadratic functions and their graphs by keeping the quadratic of the form:

,

Through investigation we will show how quadratics travel around the Cartesian Plane, find the vertex, compare x-intercepts, and compare y-intercepts.

Before we begin let us review the basic concepts and rules for vertex, x-intercept, and y-intercept

I. Vertex of a Parabola

The vertex of a parabola is the point on the graph that either contains the maximum or the minimum for the parabola (discussed later). It also is the point where the line of symmetry will travel vertically (perpendicular to the x-axis).

To find the vertex: Like all points on the Cartesian Plane the vertex is of the form (x , y). Using idea of quadratic equation and the midpoint rule we can show that:

EXAMPLE: Find the vertex of the quadratic

Solution:

The x coordinate of the vertex: a = 3 and b = -12 therefore:

By substituting x = 2 into our equation we get

We can conclude that the vertex is at the coordinate (2 , -6) and the line of symmetry is x = 2.

II. Y-Intercept

The y-intercept (abbreviated y-int) is the point(s) on a graph where the curve intercepts the y-axis. The one constant of all points that cross the y-axis is that x = 0.

To find the y-int , substitute x = 0 into your equation and solve for y. For quadratics we can come up with an easy proof for finding y-intercepts.

Remember the general equation of a quadratic is ## To find the y-int for this form all we do is substitute x = 0 and solve for y:

Therefore a quadratic function of the form:

has a y-intercept of "c" and is at the coordinate (0 , c).

III. X- Intercept

The x-intercept (abbreviated x-int) is the point(s) on a graph where the curve intercepts the x-axis. The one constant of all points that cross the y-axis is that y = 0.

To find the x-int, substitute y = 0 into your equation and solve for x. The formula for the quadratic equation is:

For any quadratic there can be from zero to two real x-intercepts. Though intercepts can be thought of in terms of imaginary numbers, for this investigation into quadratics we will focus on the real number set.

Now that the basic rules for this investigation have been reviewed to you let's look at a few different quadratics. Note for all of the tested quadratics we will show graphically the vertex, y-intercept, and the x-intercept(s) (if any). It is up to you the reader to use the rules stated above to calculate the exact values.

A) Vertex

B) y-int

C) x-int

To begin with lets look at a quadratic with a = 1 and b = c = 0

.

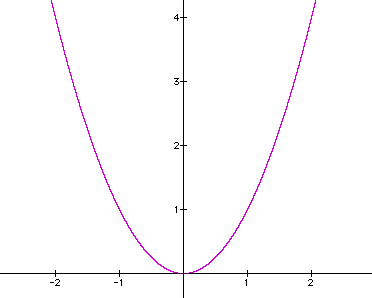
It is not difficult to visually (or algebraically) to show that the vertex of this parabola is (0 , 0) and x-int = y-int = 0.

Now we will look at what happens with change in a, b, and c individually with preset values of 1 for the other two parameters.

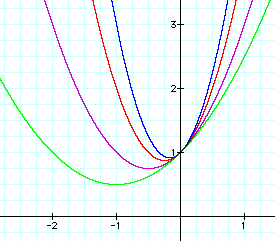
Notice that the y-intercept for all of these graphs is at the coordinate (0 , 1). Also that no real x-intercepts exist. Wish preset b and c at one we began with the first equation a =1, second equation a = 2, third equation a = 3, and fourth equation a = 1/2. By investigation we can see that as a grows from 1 to 3 the parabola "narrow" while as a goes less that one we get a wider parabola. All parabolas have a minimum value at the vertex as there are no other y values less that it. Now let's look when a < 0.

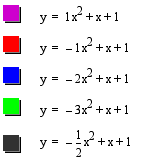
Still looking at each of the five graphs a few similarities are there. First all have a y-intercept at the coordinate (0 , 1) when a < -1 we see a narrowing parabola and when -1< a < 0 the parabola seems to widen. There are two major differences between the first graphs and the second set of it's negative a counterparts: y-values of vertex are now maximums and the direction of the curve.

Because the graphs are directed down when a < 0 we see that the y value of the vertex is the largest y value in the range of the quadratic, hence it is a maximum. Secondly and probably the most telling is that when a < 0 we see that the parabolas are directed downward.

Also you should notice that the curves for the negative value of "a" have two x-ints.

To see what happens when we vary "a" on the interval [-5 , 5]: click here

We see that the change in "a" has a bevy of characteristics for a quadratic function. The most obvious of such is the control of the direction of the parabola but also remember it aids in the placement of the vertex as well as the possible zeroes for the curve.

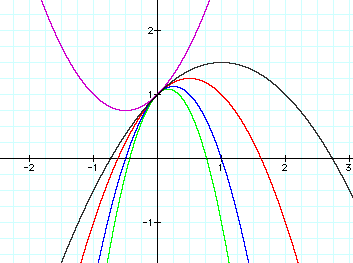
Now we will look at some different quadratics with different values put for the parameter "b"

The value of "b" has many traits that will define a specific parabola the one would notice if they looked at the rules/properties listed at the beginning of the investigation that "b" was a mainstay in vertex selection as well as the quadratic formula. With that in mind one could decide that the value of "b" has a strong emphasis on where the parabola will be placed on the Cartesian Plane.

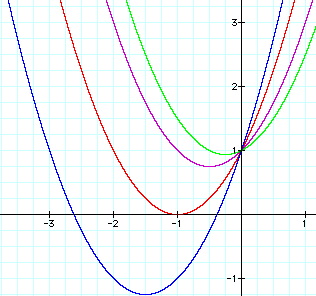
Now lets look at negative values for "b". For the sake of argument the positive value of b=1 will remain on the sketch.

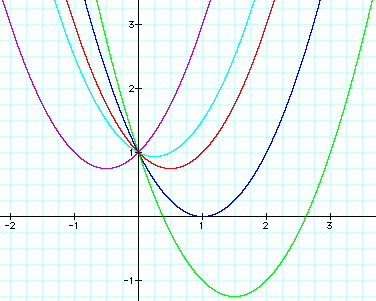
Upon looking at the curves all still have a y-int at the point (0 , 1) but the curves when b<0 have moved primarily in Quadrants I and IV. As "b" becomes more negative we would assume that the curve drops further to the down and to the right.

If we look at the curves when b = 1 and b= -1 we should see two curves that are symmetric round the line x = 0. It seems as if jumping to a negative counterpart (or positive if you started with a b<0) would give this idea with fixed values for "a" and "c"

From the beginning of the investigation we showed the "c" has a major role in the y-int of the curve. It also has control in other facets but as far as looking at "c" with fixed "a" and "b" we should see a curve that strongly resembles the others but has different y-int. Let's see.

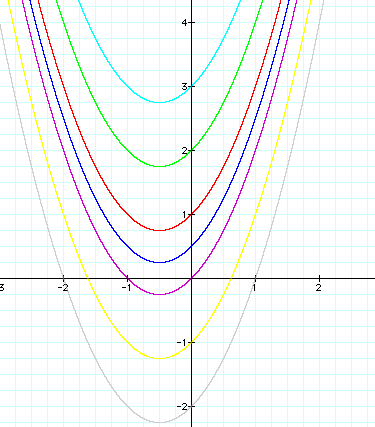
When looking at the curves we can see that as the value of "c" grows the resulting parabolas are contained within the lesser value of "c". we can also see that when c =1 and less we have two real zeroes and when c is 1/2 and higher we have no real zeroes. But there must be a value of "c" that will give the curve 1 real zero. Thus setting parameters on the two real zeroes as well as the no real zeroes for a specific equation.

Now that we have looked at the changed individually for each "a", "b" and "c" one can see that the values are the essence of the parabola. They all have aid in the control of the zeroes of the curve as well as the placement of the curve. The "c" value is the only value that has a lone specific element as it is the value of the y-int though it aids in all else.

---------------------------------------------------------------------------------------------------------------------

In conclusion, due to the vast possible changes one can do with the values of "a", "b", and "c" one cannot fully see all the possibilities but hopefully this has helped you see ideas that make up a parabola. If there are any questions please contact me back by email back on my web page.

BFM

Return to Brock F. Miller Page