
Orthocenters

The purpose of this investigation is to form conjectures and proofs about the relationships between triangles made up by the orthocenter and vertices of the parent triangle and the parent triangle of the orthocenter and the circumcircles of the three triangles and the parent triangle. To start we will define the orthocenter of a triangle as the intersection of the three altitudes of a given triangle. The orthocenter is labeled with an H.
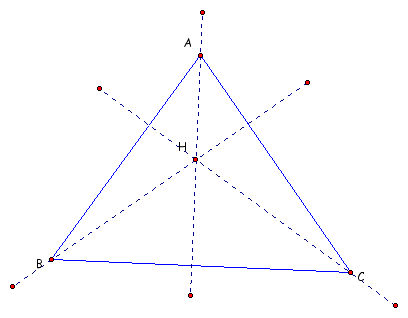
For this triangle ABC the orthic triangles are HAC, HBC and HAB. Visually:
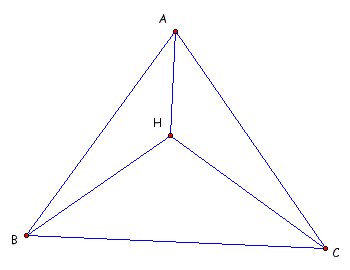
Clearly from the pictures and the definitions
of orthocenter and segment we can conclude that segments HA, HB,
and HC lie upon the three altitudes of a the triangles.
CONJECTURE - The orthocenter of a triangle made up of the orthocenter and two of the parent triangle's vertices is the third vertices of the parent triangle.
Let's examine triangle HBC, by our conjecture the orthocenter of this triangle is point A
PROOF:
We know the orthocenter is the intersection of three altitudes of the triangle. We know that HA lies on the altitude from A to BC therefore the line containing the altitude from H to BC is the same:
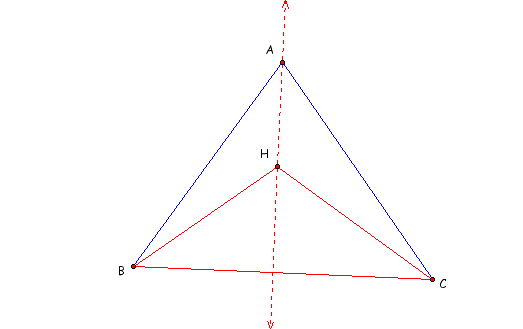
Next is construct the altitude from C to HB. We notice that angle BHC is obtuse therefore the altitude will not be on segment HB but on the line containing HB, which in fact is the altitude from B to AC.
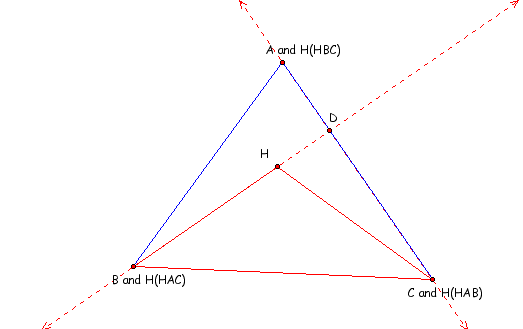
By definition of the orthocenter we know that line BD is perpendicular to segment AC at point D. Therefore a line running from point C perpendicular to BD is also perpendicular at D. We know that D is on segment AC therefore the altitude traveling from C to line BD would also include the segment AC. Visually:
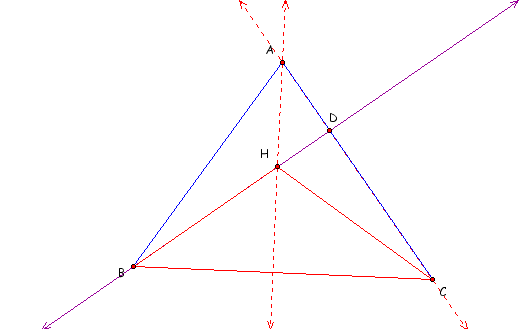
Likewise can be shown with the line containing the altitude from B to CH:
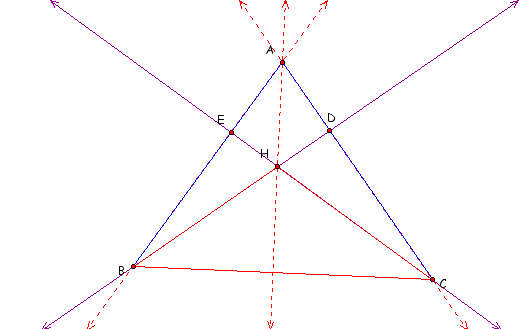
Therefore because that line AB contains side AB and line AC contains line AC and line AH contains point A we can find the intersection of the three sets easily as being point A.
Proving the other two orthocenters goes along
accordingly with the first proof.
Now since we have proved this it is should be clear that the orthocenters to the three smaller triangles are so:
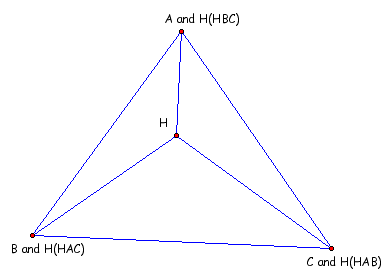
For GSP 4.0 Users - To manipulate the picture
Click Here
The circumcircle of a triangle if the circle that touches a triangle only at it's three vertices. To find the center of the circumcircle of a triangle (known as the circumcenter) one must find the point of intersection of the perpendicular bisectors of the three sides.
Circumcircle of triangle ABC with a center labeled C1
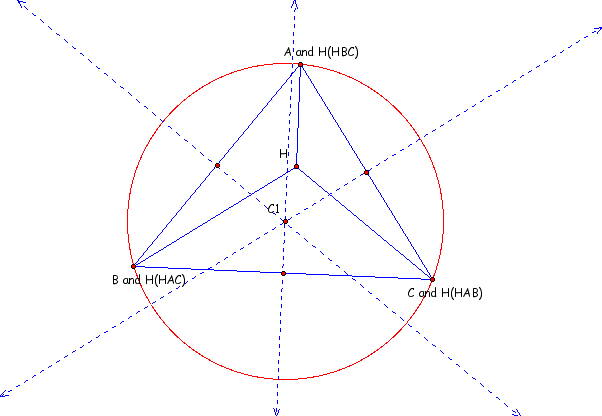
Circumcircle of triangle HBC - center C2
Circumcircle of triangle HAC - center C3
Circumcircle of triangle HAB - center C4
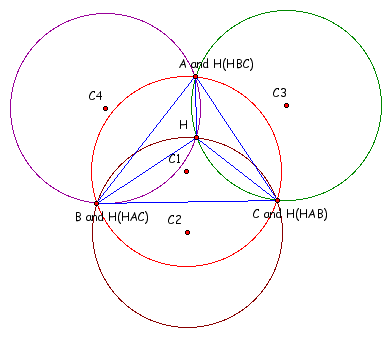
GSP 4.0 Users - To manipulate the figure Click Here
CONJECTURE - All four circles
have the same area
To show this we must prove that the radius of each circle are equal to that of the other three.
Though this is not a proof we can use the Measure feature to check the areas
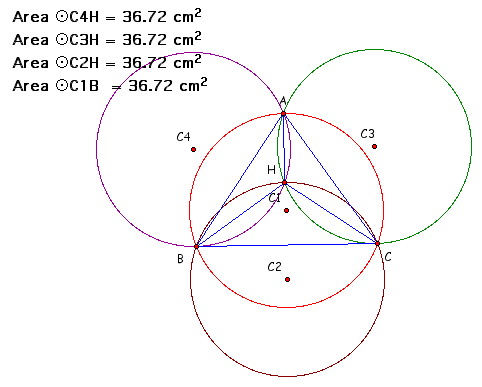
We see that numerically for this situation our conjecture is correct but let's see if we can prove it: Let's try to prove circles C4 and C3 have the congruent radii.
We will focus on just circles C4 and C3 so for the time being we will hide circles C1 and C2.
Notice that Circles C4 and C3 both intersect at A and H. So we will construct segments from the two centers to those two points.:
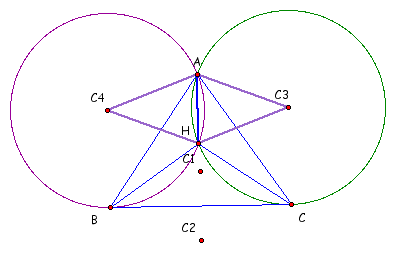
Now if we construct parallel lines to BC running through H and A as well as parallel l lines running through C4 and C3 and a line running through C3 and C4 we get this picture (Note that we have hidden some other pieces to aid in the viewing)
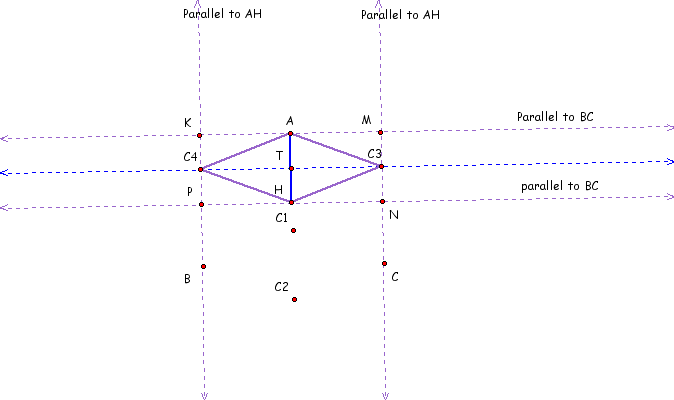
Due to parallel lines we know we have right angles at the intersections of lines at points K, M, N, P. Therefore by rule KMNP is a rectangle.
Also because by definition of a circle that C4A = C4H and C3A = C3H.
Therefore triangles C4HA and C3HA are isoceles making line C3C4 perpendicular as well as a bisector of AH.
By definition of a rectangle KATC4 and AMC3T are rectangles making KC4 = AT as well as AT = MC3
Therefore by the transitive property KC4 = MC3.
By putting to use the parallel lines m<KC4A = m<MC3A
Therefore Triangles KC4A and MC3A are congruent by leg-angle postulate of congruence.
which means that AC4 = AC3 by corresponding parts.
Therefore Area of Circle C4 = Area of Circle 3.
Likewise can be shown for all other circles
Therefore: Area of Circle 1 = Area of Circle 2 = Area of Circle 3 = Area or Circle 4.
I have convinced myself of this fact. I acknowledge that it is a bit scattered but if you have an easier proof to show me please email it to me.
BFM
RETURN to Brock F. Miller Page