---

Pedal Points

and

Pedal Triangles

by

Brock F. Miller

This investigation into pedal points and pedal triangles will attempt to clearly show:

I. Pedal Point and Pedal Triangle Construction,

II. Different Loci of the Pedal Triangle in comparision to the Pedal Point, and

III. The Pedal Point compared to other centers of a triangle.

PEDAL POINT SCRIPT TOOL

Initially let's define a pedal point.

Pedal Point - the point of intersection of the lines perpendicular to the lines containing the sides of a triangle.

The construction is quite simple. First start with a triangle and an aribitrary point off the triangle.

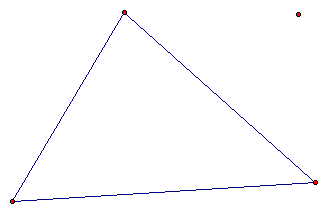
Now since the pedal point is perpendciular to the lines containing the three sides of we need to extend the sides of the triangle as so:

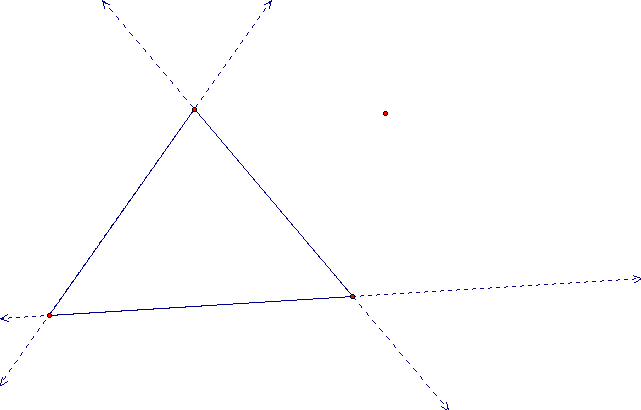
Now we will construct the perpendiculars and their respective points of intersection.

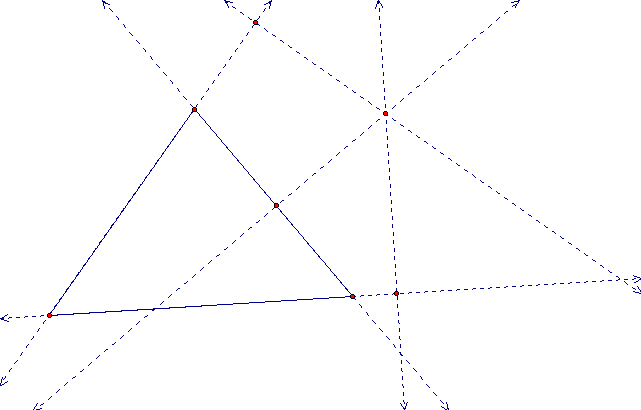
These three points of intersection are the vertices for the pedal triangle. Clearly:

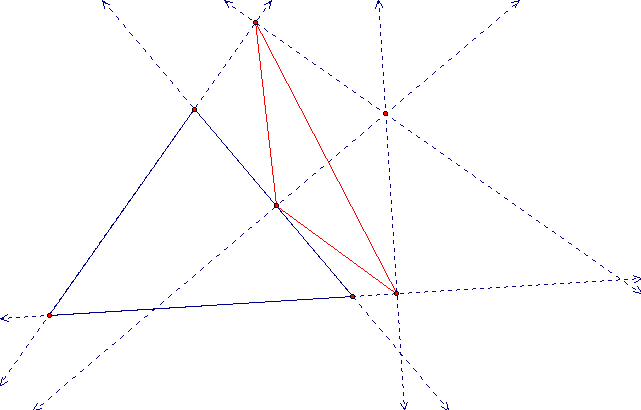
At this point the dashed lines are little use to us so we can eliminate them to form our pedal triangle.

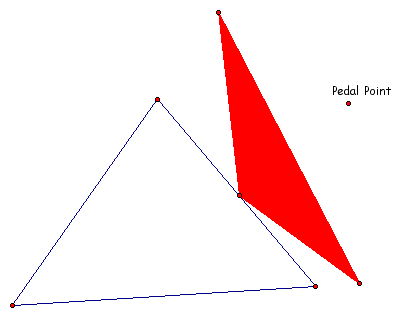
Since the pedal point is an arbitrary point we can move it around anywhere in the plane.

EX I

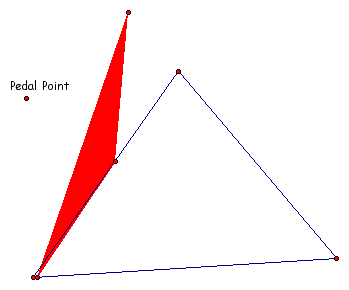
EX II

(Note just a change in color to make the pedal point clearer)

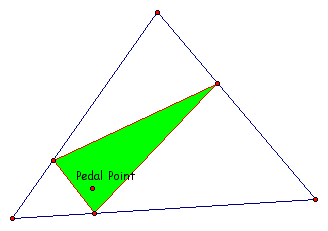
Locus I - 1 Midpoint

It appears as if the locus of the midpoint is that of an ellipse. Now let's compare the loci of the three midpoints of the pedal triangle.

Locus II - 3 Midpoints

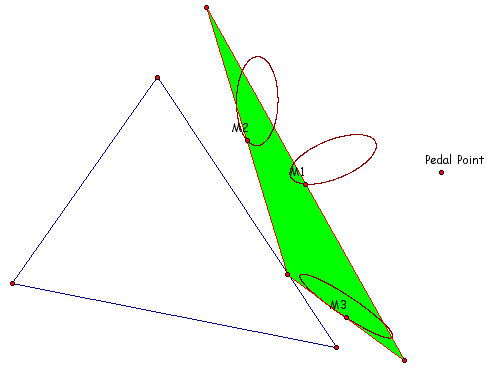
It appears as if all three loci are ellipsi. Notice it does not matter even though we changed the magnitude of the parent triangle.

Not let's change the path of the pedal point and put the path on a circle that contains the circumcenter, C, of the parent triangle

First let's put the pedal point on a circle larger than the circumcircle of the parent triangle.

Locus III - 3 midpoint

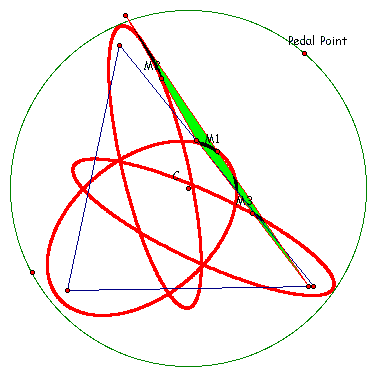
It still appears to be three ellipsi. So lets make the circle smaller than that of the circumcircle.

Locus IV - 3 midpoints

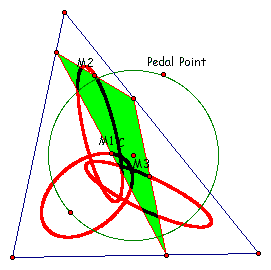
Still not much has changed it still appears to be three ellipsi. Now let's put the pedal point on the circumcircle of the parent triangle:

Locus V - 3 midpoints

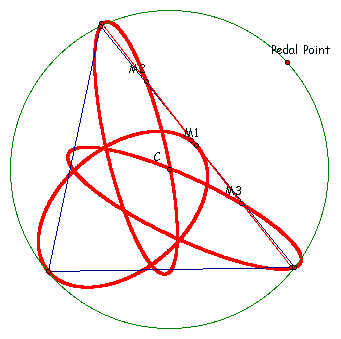
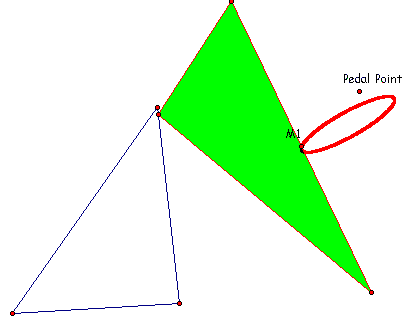
Though the loci seem to mirror all other previous examples the interesting thing is that the parent triangle has collapsed into what appears to be a line. In fact it does. A brief explanation:

Consider the case when the pedal point and the circumcenter are collinear.

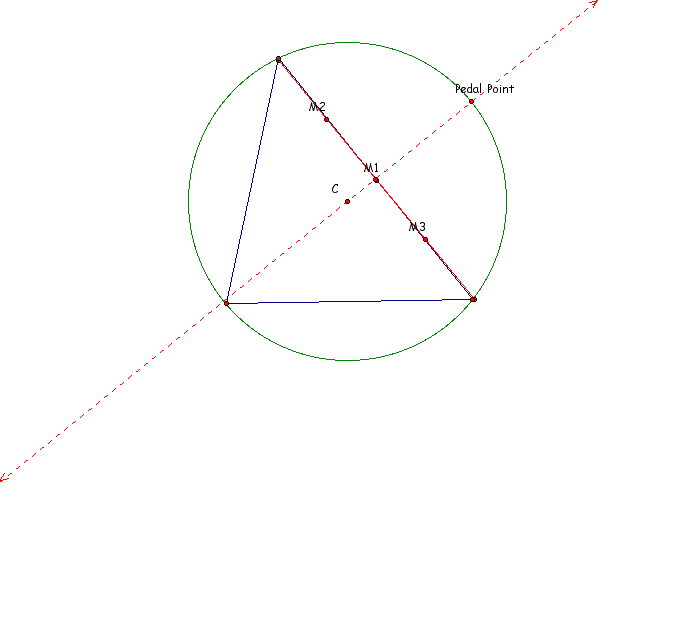
By figure it appears that two of the vertices of the pedal triangle intersect two of the vertices of the parent triangle. as well as the three midpoints lie on a side of the parent triangle. The pedal point and the M1 lie on this perpendicular. since M1 is a midpoint it follow that the figure created by this situation is that of an isoceles triangle:

Hence the pedal triangle has collapsed into the base of an isoceles triangle with the pedal point as it's point of location of the vertex angle of the isoceles triangle.

This look at the loci of the pedal point and pedal triangle is a small look into what can be numerous investigations and proofs. Though we looked at a few examples what about others: the quarter points of the pedal triangle sides? the centers of the pedal triangle? maybe even looking at this in three dimensions? Feel free to go on and enjoy.

CASE I - Pedal Point vs Orthocenter of the parent triangle

By definition the orthocenter is the point of intersection of the three altitudes of a triangle meaning it it perpendicular with the sides. The resulting points of intersection with he sides of a triangle create the orthic triangle.

ORTHOCENTER (H) and the ORTHIC TRIANGLE:

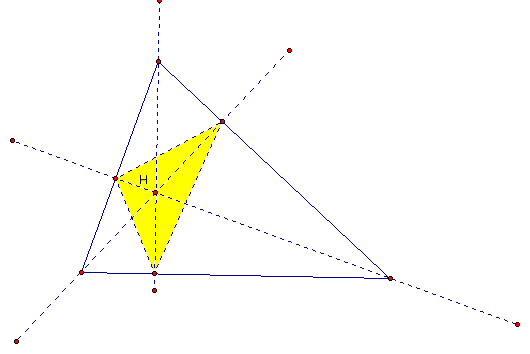
Earlier we defined the pedal triangle as the union of the points of intersection with an arbitrary point (pedal point) and the line containing the sides of a triangle. Clearly these definition have some intersection. In fact the orthic triangle is an example of a pedal triangle since it matches in definition making the orthocenter an example of a pedal point. So if we were to create a figure with an orthic triangle and a pedal triangle when the pedal point is moved on to the orthocenter the pedal triangle and orthic triangle will sit directly on top of each other. In fact by early definitions I have read that would correspond to congruency.

GSP 4.0 Users - Move the pedal point on to the orthocenter and visually show this. CLICK HERE

Case II - Pedal Point vs the Circumcenter of the Parent Triangle.

By definition the circumcenter is the point of the intersection of the perpendicular bisectors of the sides of a triangle. The resulting point will be the center of a circle that crosses the triangle at it's vertices.

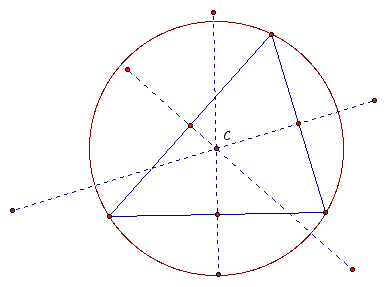
Clearly if the pedal point was the circumcenter the orthic triangle would be made up of the midpoints of the sides of the parent triangle.

GSP 4.0 Users - Move Pedal Point to the Circumcenter (C) and show this: CLICK HERE

CASE III - Pedal Point vs the Incenter of the parent triangle.

Upon looking at the definition of the incenter of a triangle one might not think that there would be any relation between the these two ideas. Let's take a look:

By definition the incenter is the point of intersection of the three angle bisectors of a triangle.

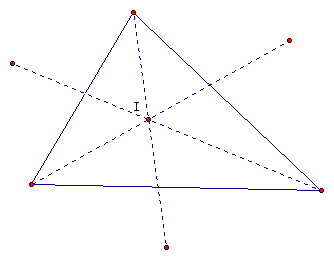
The incenter is the center of the circle that is inscribed in a triangle. This circle will intersect the triangle at three points. These three points run from the incenter perpendicular to the sides:

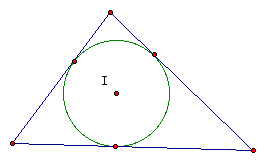
Clearly that if the incenter is on the line perpendicular to the sides of at the points of intersection that if we chose the point I as a pedal point then these three points of intersection would be the vertices of the pedal triangle.

GSP 4.0 Users - Move pedal point to the incenter, I, to convince yourself. CLICK HERE

CASE IV - Pedal Point vs Center of Gravity

After looking at these two ideas I could not find much interesting except at specific cases of parent triangles, ex isoceles or equilateral. Maybe you can. Find one and email it to me.

I hope this look at pedal triangles and pedal points has been interesting. I hope that you understand the connections I have made in this write-up. If you have any questions or comments please email me from my home page and let me know.

BFM