
Assignment 1: Graphs
Exploring Linear Combinations
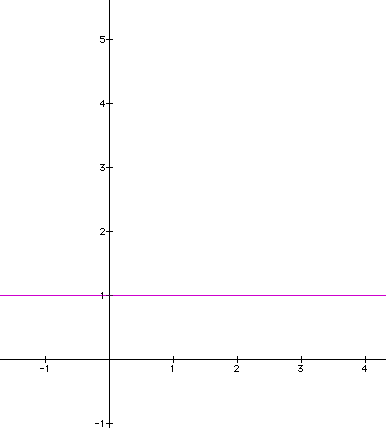
Here is a graph of the
line y =
1
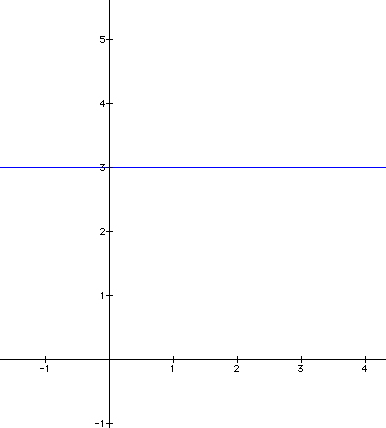 And this is a graph
of the line y
= 3
And this is a graph
of the line y
= 3
In arithmetic, we are
accustomed to ADDING and SUBTRACTING.
We can also add and subtract (so to speak) lines and other functions.
So, we can ADD y = 1 and y
= 3.
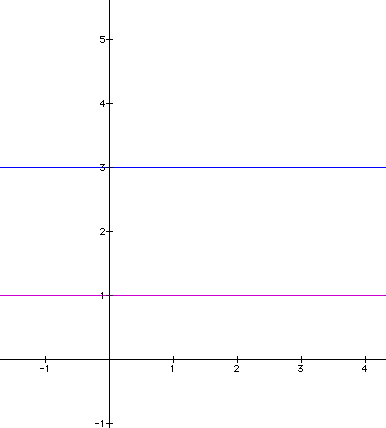 What might ADDING mean
with reference to LINES?
What might ADDING mean
with reference to LINES?
The red line shown in the graph below can be
viewed as the result of
ADDING y
= 1 and y = 3.
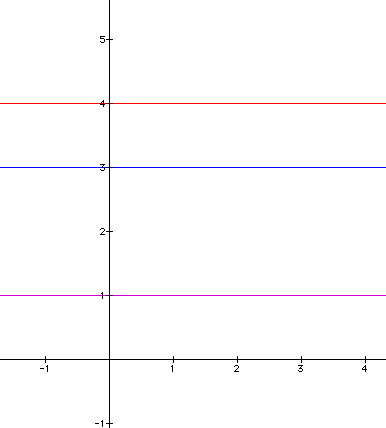 Can you determine how
y = 1 and y = 3 were
added to "create" the red
line?
Can you determine how
y = 1 and y = 3 were
added to "create" the red
line?
Does the following graph
help make sense of adding the lines?
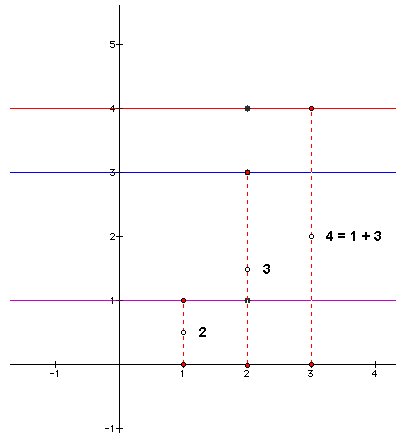
To get an idea of what is going on
in a more formal sense, let's rename the two equations we started
with.
Rather than y = 1 and y = 3,
let's change the notation so we can be sure that we are always
talking about two different lines, like this:
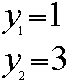
When we ADD two lines, we can say that
we add
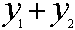 So, we have
So, we have
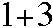 and, of course,
and, of course,
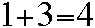
But, what does that
"4" mean?
When we add two lines,
what do we get?
In other words,
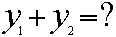
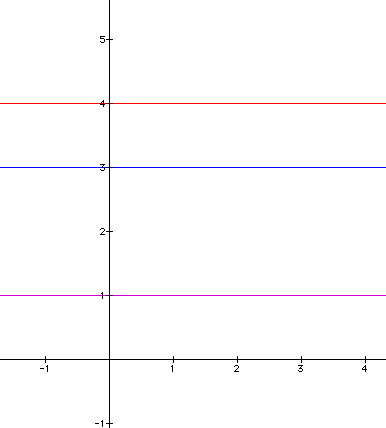 Remember we said that
this graph represents the addition of y = 1
and y =
3
a
So when we add two lines,
Remember we said that
this graph represents the addition of y = 1
and y =
3
a
So when we add two lines,
we get another line
a
In this case, we "created"
a line
y = 4
So to answer the question:
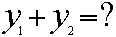 We can respond with:
We can respond with:
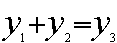
But, is it clear what
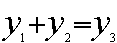 means?
means?
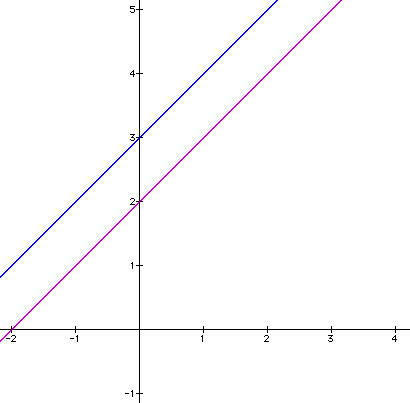
Let's try these two linear equations:
y=
x + 3
and
y = x +
2
What do you think we will get by adding
these two linear equations?
Did you come up with
something like this?
Is this a "good"
solution?
How can we tell?
Think again about the
relationship
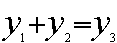
If 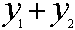 , we need:
(x+ 2)
+ ( x+ 3)
, we need:
(x+ 2)
+ ( x+ 3)
What
do you get now?
Did you get something
like this?
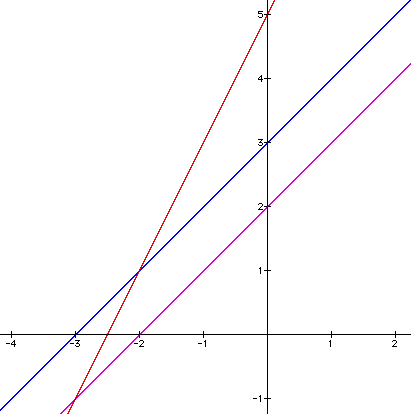 What is the equation
of the red line?
What is the equation
of the red line?
y =
2x + 5
Do you understand why?
Need help? Click here 
Do you have an interpretation
of how these line all relate to each other?
Let's go back to the question
of what 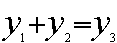 tells
us.
tells
us.
Remember that we identify points
on a line with coordinate pairs and that this is a fancy
term meaning that any point has an x-component and a y=component.
So the equation 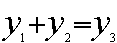 tells us to add the y=components.
tells us to add the y=components.
Let's take another look at the
equations y=
x + 3 and y = x + 2 when
x = 0 and x = -2.
When x = 0, y= x + 3
becomes y=
0 + 3 = 3.
Similarly, at x = 0, y = x + 2 becomes y = 0 + 2 = 2.
In this case, 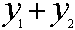 gives us 3 + 2 = 5.
gives us 3 + 2 = 5.
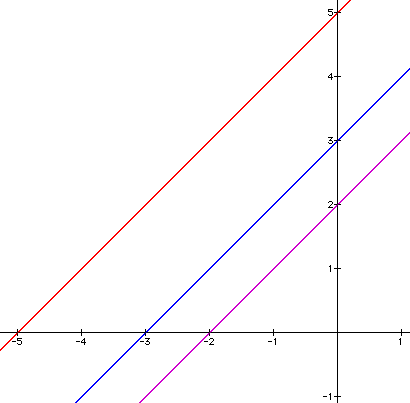
Look at the graph above again:
What is the y-value of the red
line at x = 0?
At x = 0, y = 2x + 5 = 5
When x = -2, y= x + 3
becomes y=
-2 + 3 = 1.
Similarly, at x = -2, y = x + 2 becomes y = -2 + 2 = 0.
And y = 2x + 5 becomes
y = 2(-2)
+ 5 = -4 + 5 = 1.
Look again at
the graph: Does the result y = 1
for y =
2x + 5 seem
correct?
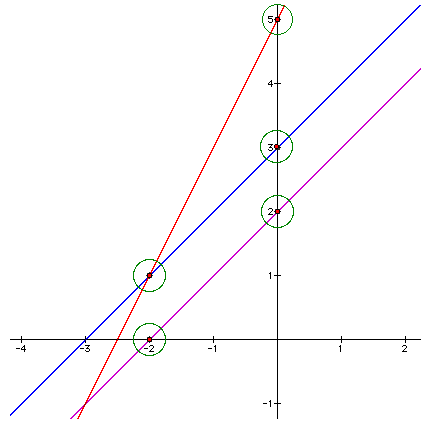
Here
is another look at the same three lines
As you
move
a point along the horizontal axis,
how do the y-values for the three
lines relate to each other?


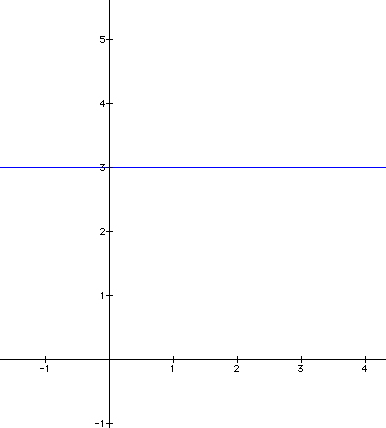
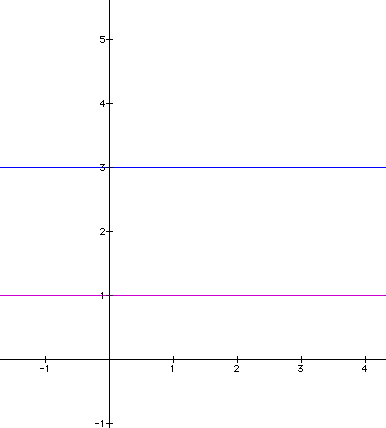
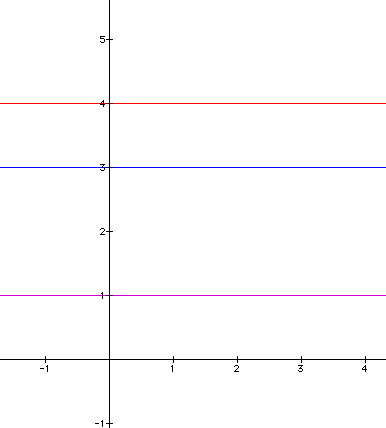

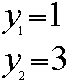
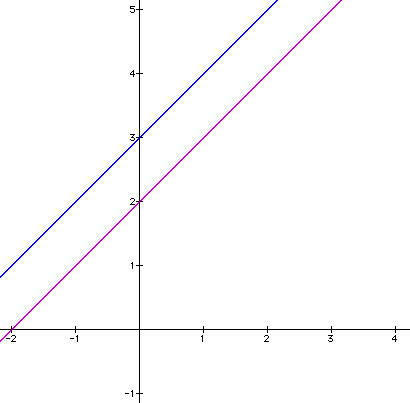


![]() tells
us.
tells
us.![]() tells us to add the y=components.
tells us to add the y=components.![]() gives us 3 + 2 = 5.
gives us 3 + 2 = 5.