Assignment 4:
Concurrencies of a Triangle
Relative Locations of Triangle
Centers
A Centroid is
formed in a triangle by the intersection of segments from the
MIDPOINT of the SIDES to the OPPOSITE VERTEX, like this:
Think about how the Centroid
is constructed.
Do you think the Centroid is always on the Interior of the Triangle?
How can you test your thoughts?
Take a look at an animated
version of a Triangle with its Centroid.
Can you explain why the Position of the Centroid behaves
the way it does as we change the Triangle?
An Orthocenter
is formed in a triangle by the intersection of the ALTITUDES:
We can construct the Orthocenter
by making lines Perpendicular from each side to the Opposite vertex,
like this:
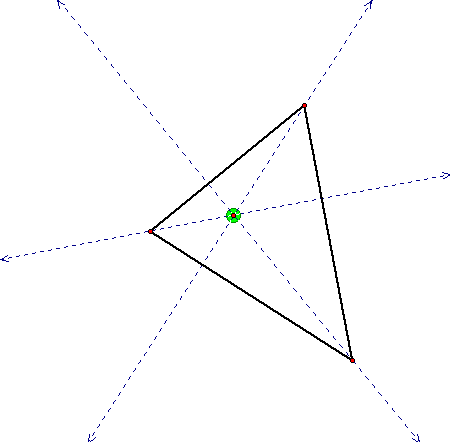
Do you think the Orthocenter
is always inside the Triangle?
Why does the Othocenter move the way it does?
(It may help to consider how the Orthocenter is constructed.)
Need Help? Click below.
The Circumcenter
is formed by the intersections of the
PERPENDICULAR BISECTOR to Each Side of the Triangle, like this:
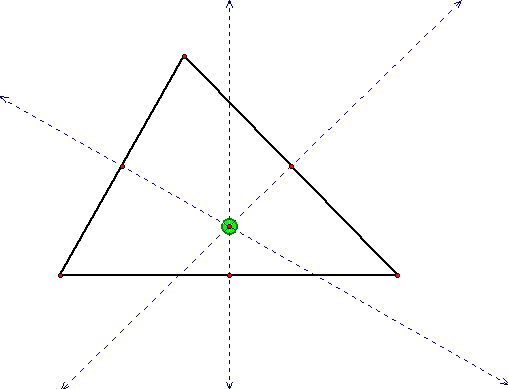
Do you think the Circumcenter
can ever lie on the Exterior of the Triangle?
Take a look at the animation.
Did the Circumcenter behave the
way you expected it to?
Can you explain why it behaves the it does?
Need Help? Click below.
We can construct any Triangle
within a Circle:
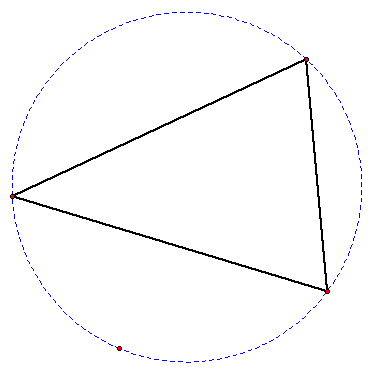
n
What do you think might happen
to the Centroid, the Orthocenter,
and the Circumcenter as we adjust the Triangle within
the Circle? That is, if we move any vertex of the Triangle around
the Perimeter of the Circle, how will the Centers behave - will
they lie inside or outside the Triangle?
n
Take a look at the
animation below.
It shows a Triangle
inscribed in a Circle and
There are several points labled: A, B, & C.
Based on what you saw in the discussions above,can you determine
which Triangle Centers are represented by A, B, & C?
Try adjusting point
X around the circle:
What observations can
you make about the relationships between the Triangle, the Centers,
and the Circle?