Problem: Coloring
Circles (click here to see the problem statement)
My solution.
I can first observe that the center circle is initally irrelevant
in that it is constrained only by the color of the circle in the
upper-left to which it is connected and in no way constrains the
coloring of any other circle. Therefore, I can focus on the four
circles that are connected in a cycle.
I begin by fixing the color of the upper-left circle and the
lower-right circle and constrain the choices to two colors.
In this way, I obtain six colorings:
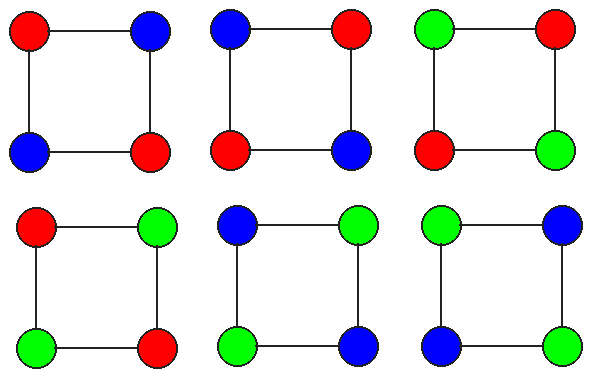
I then fix both the upper-left and lower-right circle and
allow three colors:
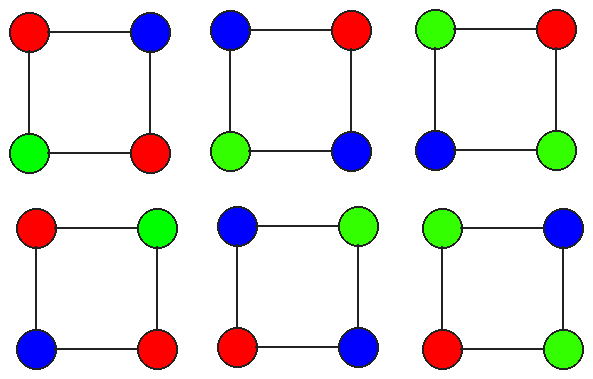
In the final coloring, I fix only the upper-left circle and
allow three colors in the graph:
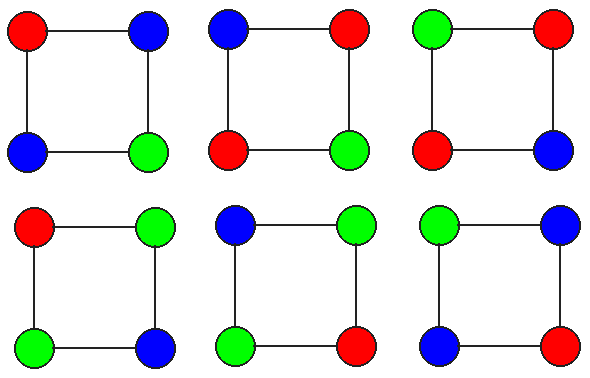
In this way, I have obtained 18 colorings. However, at this
point, I need to consider the center circle. The coloring of the
center circle is constrained only by the color of the upper-left
circle and given three colors, any individual color can be matched
with either of the other two colors.
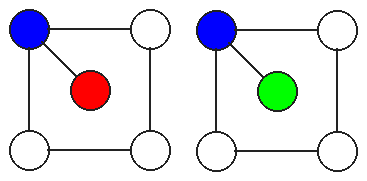
So each of the 18 the colorings obtained above has two additional
possibilites for center circle coloring, resulting in a total
of 36 distinct colorings.




