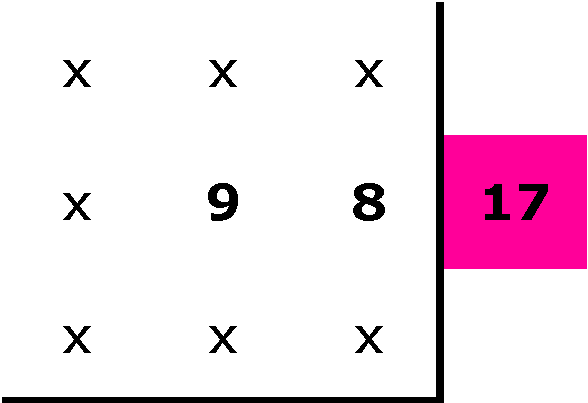Problem. Magic
Square (click here to see the problem statement)
My Solution
(Basic Square).
I can use only the whole numbers 1 through
9. I start by making a 3x3 array of those numbers:
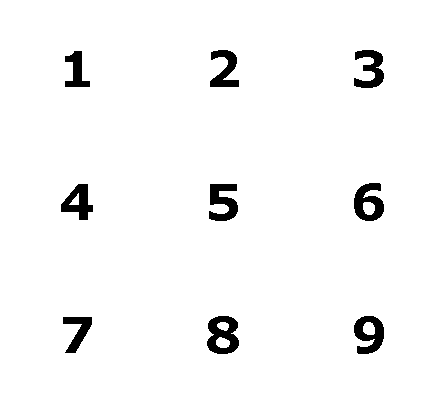
I need to get an idea of how the sum
are interacting, so I add up each row, column, and diagonal. I
find that the middle row, the middle column, and both diagonals
sum to 15:
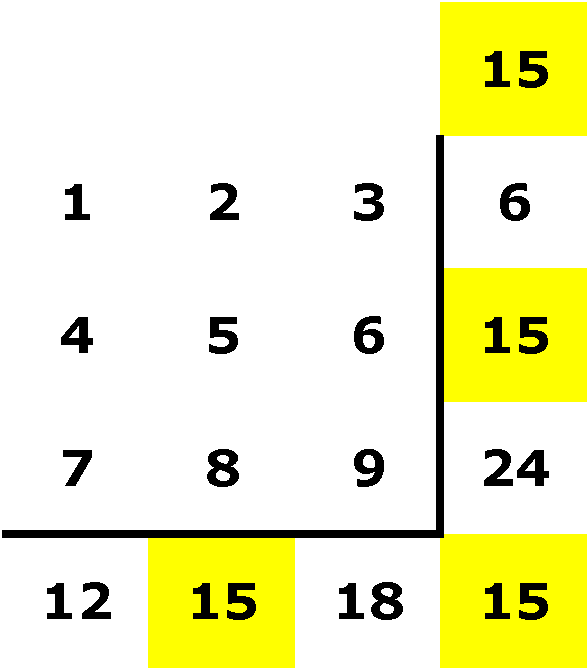
The sum of the first row is 6 and the
sum of the third row is 24. I need to balance the results, so
I try switching the 2 and the 8 in the middle cloumn:
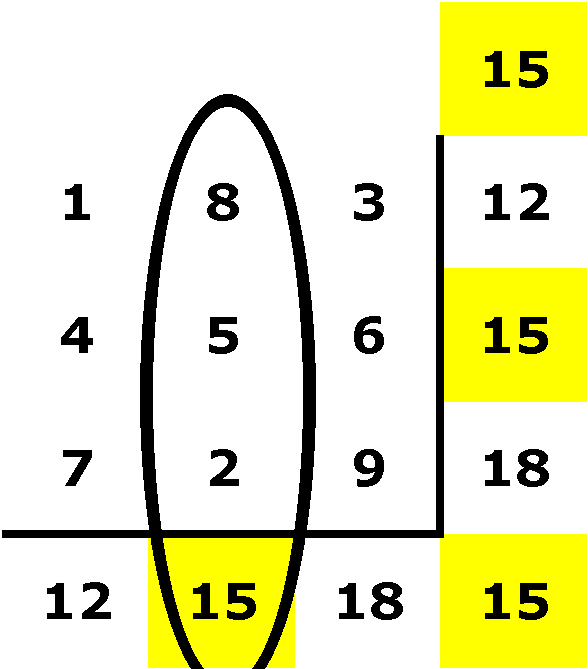
I try to balance the first and third
columns more by switching the 4 and 6 in the midle row:
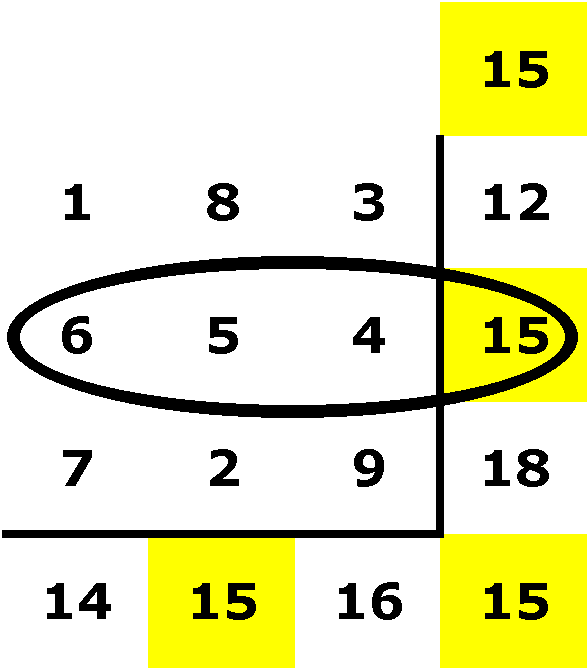
As 5 is in the middle square and I am
trying to achieve a sum of 15 in all cases, I need to maintain
pairs on the "outer ring" that each add to 10: (1,9)
(2,8) (3,7) (4,6) and that are in opposite positions on the outer
ring. I try rotating the outer ring counter-clockwise:
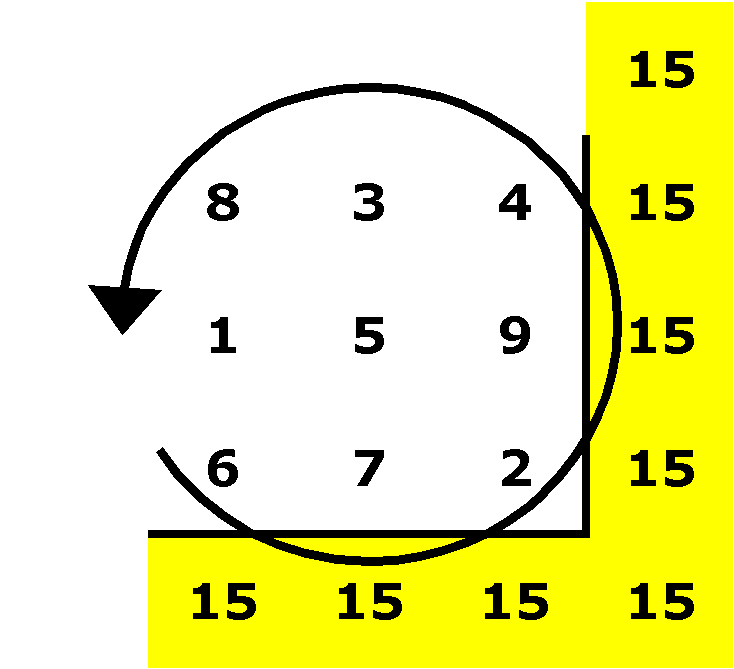
I luck out on my very first rotation.
I try again:
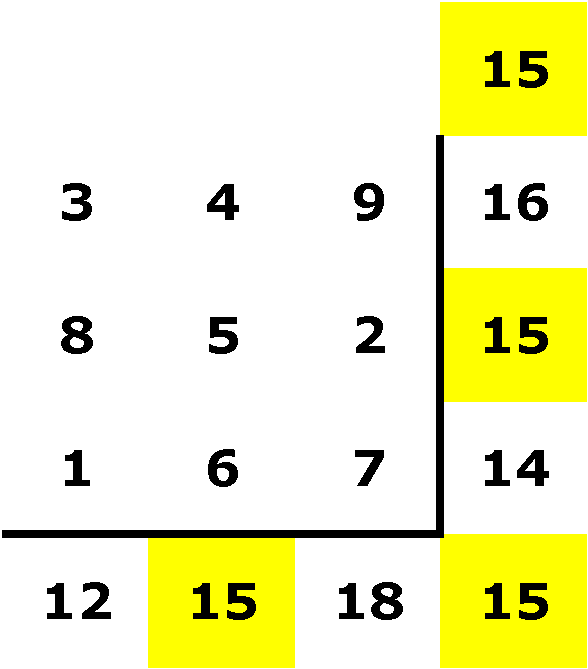 then
then 
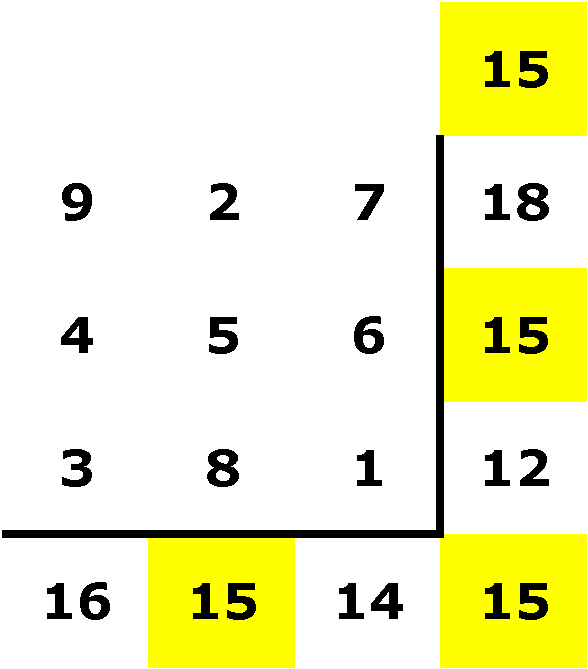 then
then 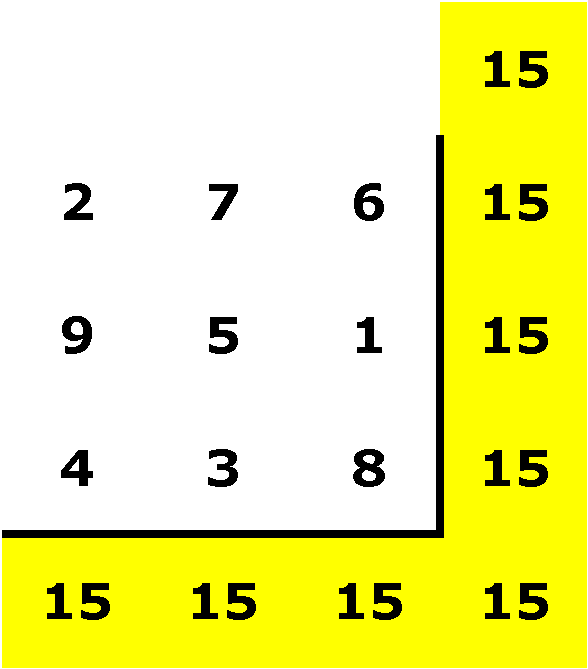
 then
then 
 And the next rotation will bring the ring full-circle.
And the next rotation will bring the ring full-circle.
So it appears that my solutions are:
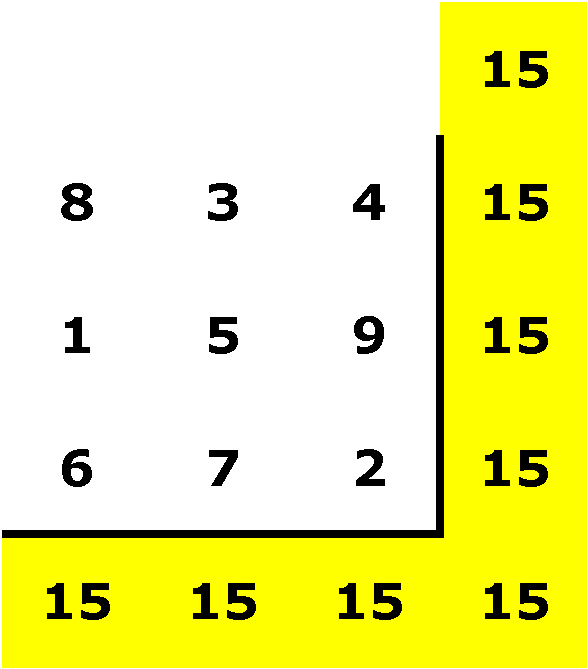



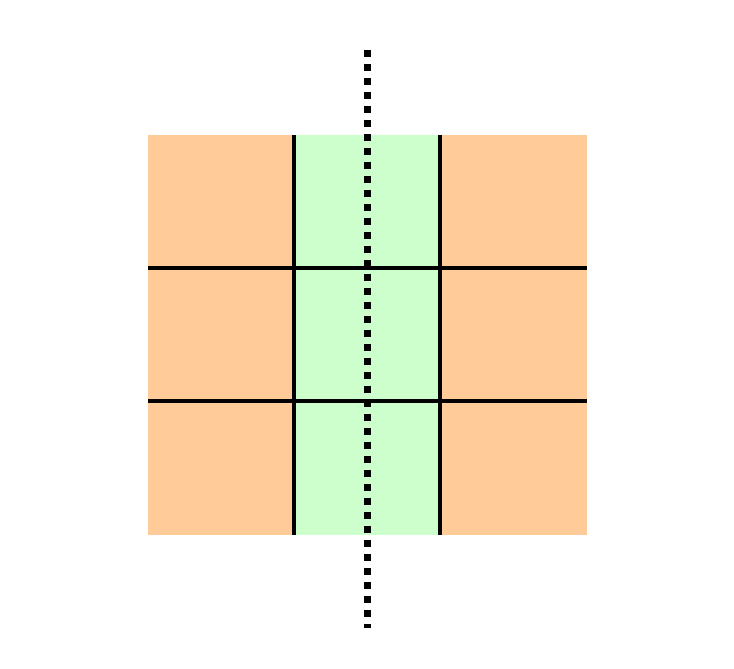
I now need to consider possibilities
other than rotations, so I can examine Reflections. For example,
I can hold the middle column constant and switch the numbers in
the the first and third columns:
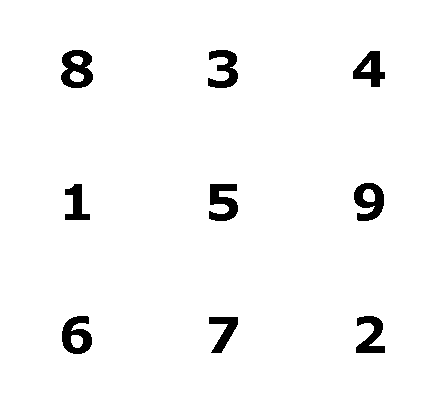
If I define this array to
be my base,
then a reflection about
the middle column is: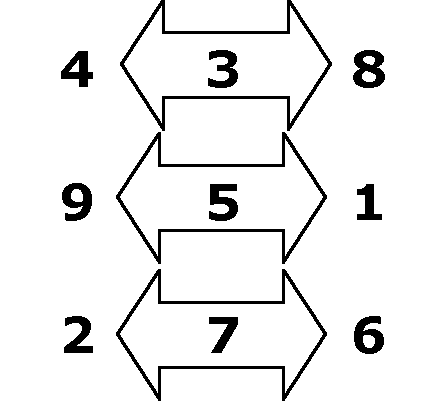
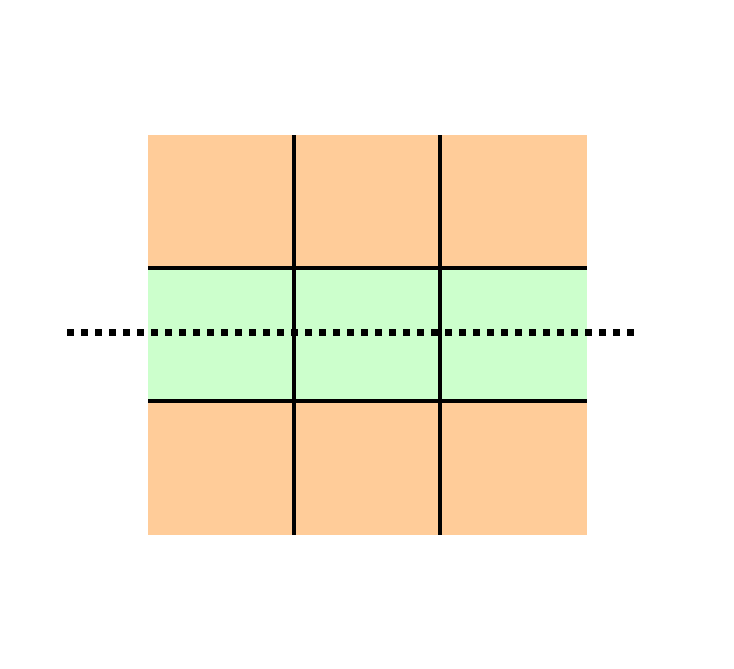
Similarly, a reflection about
the middle row
means that I hold the middle row constant
and switch the numbers in the first and third rows:
So my reflection is: 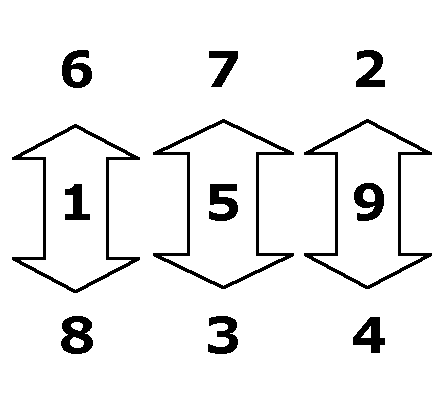
And reflections about each diagonal:
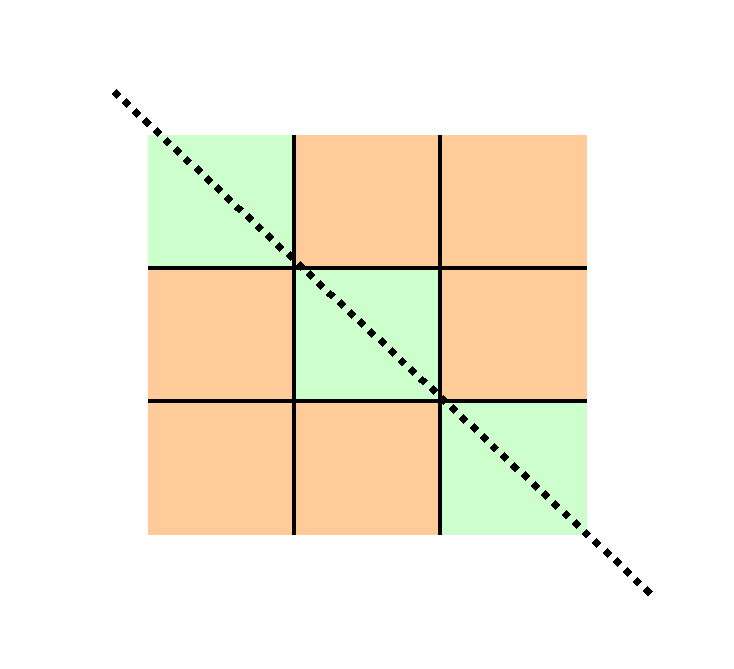 gives
gives 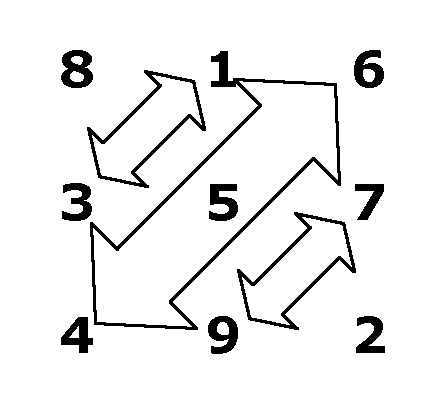
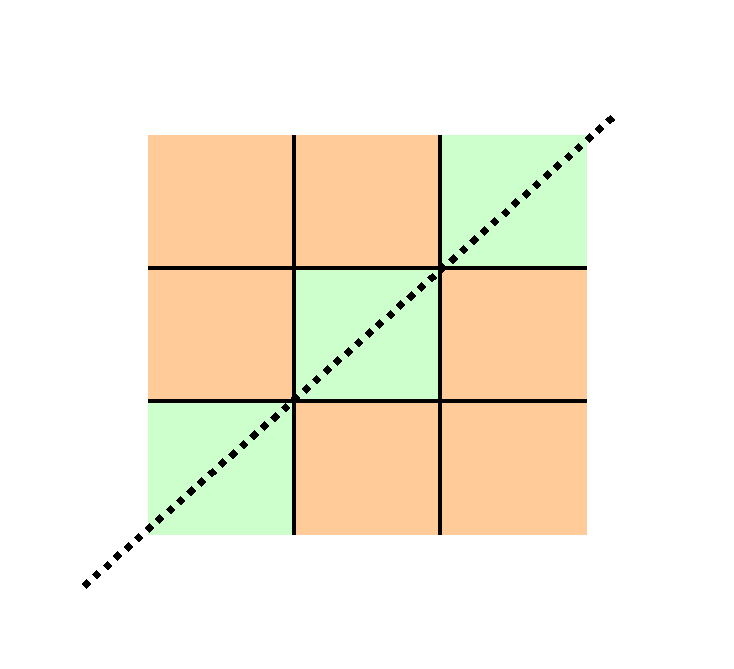 gives
gives 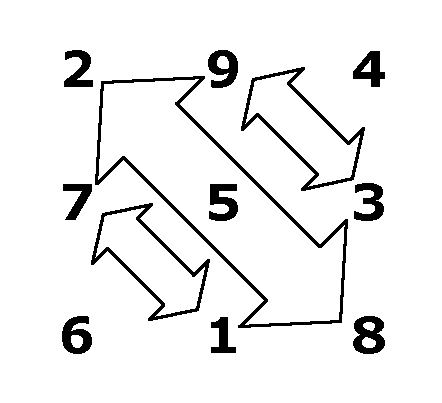
Last, I need to examine the possibility
of placing numbers other than 5 in the middle square, such as
8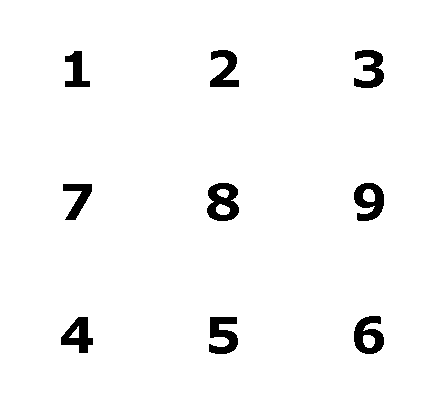
I can fairly quickly determine that this
is not an option, because I will have 9 somewhere in the outer
ring. As the sum of 8 & 9 is 17, I will have a row or column
greater than 15. I can immediatley extend this to rule out having
9 in the middle square:
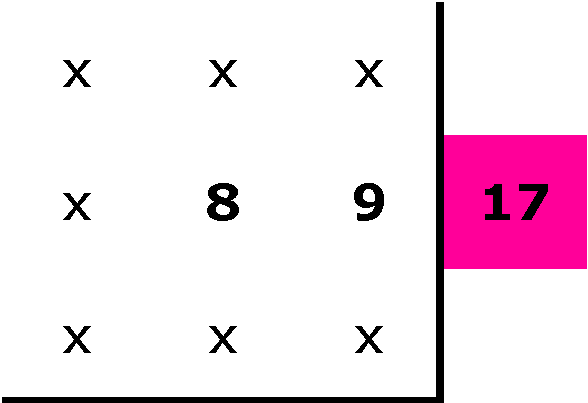 -&-
-&- 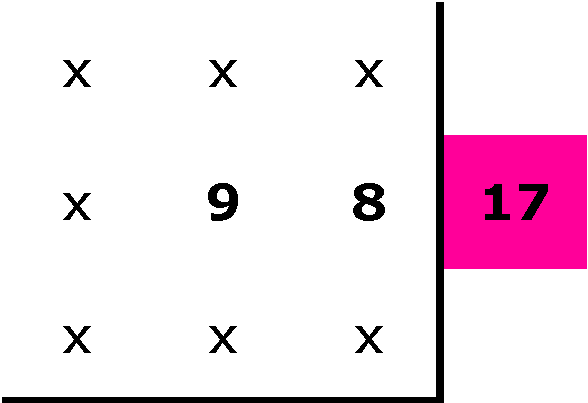
For 7 in the middle square,
I need the sum of all pairs of remaining numbers to equal 8; however
in my set
{1, 2, 3, 4, 5, 6, 8, 9},
I already have 8 and 9, so there will be at least one pair whose
sum is breater than 8.
For 6 in the middle square,
the sum of all remaining pairs must equal 9;
however my set contains 9, so there is at least one pair whose
sum is greater than 9.
For 4, 3, 2, or 1 in the middle
square, the sum of all pairs must equal 11, 12, 13, and 14,
respectively;
however in each set we have 1, 2, 3, and 4 requiring the matches
for each to be 10 (or greater),
none of which is included in the set.
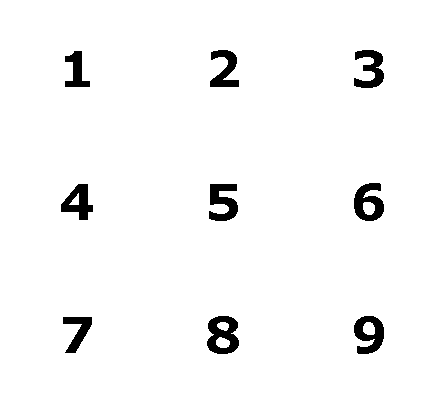




 then
then 
 then
then 
 then
then 
 And the next rotation will bring the ring full-circle.
And the next rotation will bring the ring full-circle.




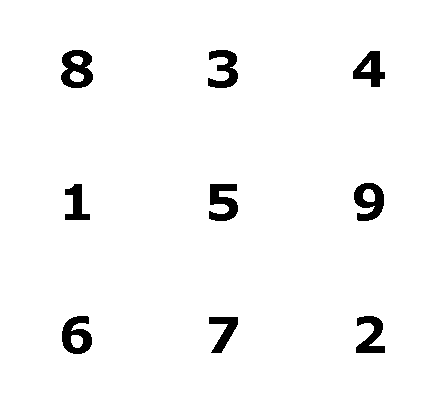


 gives
gives 
 gives
gives 
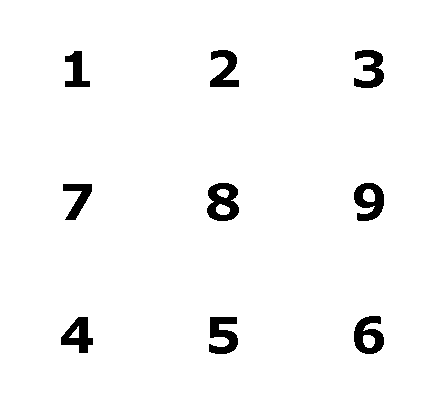
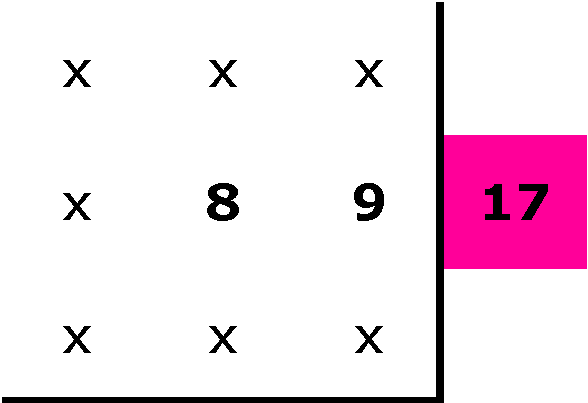 -&-
-&-