

For the final assignment, we were to take any triangle ABC and choose a point P in the interior of triangle ABC and then draw lines AP, BP, and CP so that they intersected the side opposite the vertex from which they were drawn. This has been done below.
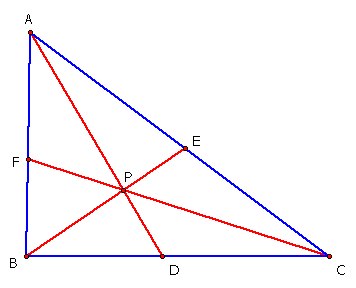
Given this triangle and these lines, we were to explore the relationship between (AF)(BD)(CE) and (FB)(DC)(EA) for various shapes and sizes of triangles. Explore this relationship.
As you can see, it appears that (AF)(BD)(CE) always equals (FB)(DC)(EA) for any shape or size of triangle.
How can I prove this conjecture? Well, this proof is rather simple if one is familiar with cevian lines. A ceva line is any line that passes through a vertex of a triangle and a nonvertex point on the side of the triangle opposite that vertex. As you can see from above, lines AD, BE, and CF all fit this form, and in fact, they are all cevian lines. So, what about the proof?
Well, from geometry, there is a theorem that tells us that when any three cevian lines are concurrent at a single point, then there is a ratio that is true for any triangle. Well, it is obvious from above that the three cevian lines, AD, BE, and CF are concurrent at P. Therefore, the ratio will hold. The ratio is the following:
When (FB)(DC)(EA) is multiplied to both sides, the equation is (AF)(BD)(CE) = (FB)(DC)(EA).
Therefore, as was conjectured above, (AF)(BD)(CE) always equals (FB)(DC)(EA).
Now, does this relationship hold if P is not in the interior of triangle ABC? Explore this and see what you find! Move A, B, C, or even P to see this relationship.
For the last part of the assignment, I explored the ratio of the areas of triangle ABC and triangle DEF. For this part, P was in the interior of triangle ABC. A picture of this is below.
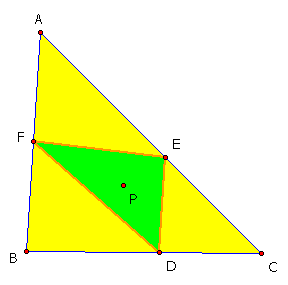
It turns out that the ratio is always greater than or equal to 4. Explore this relationship.
There is one place where the ratio is exactly 4. This is shown below.
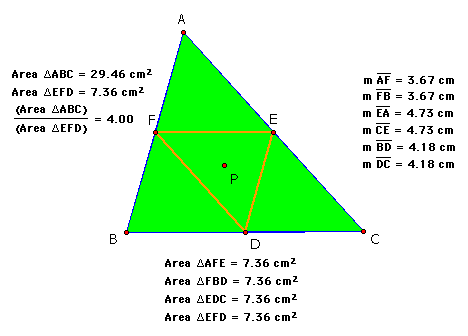
Notice that F is the midpoint of AB, D is the midpoint of BC, and E is the midpoint of CA. Therefore, P is the centroid of triangle ABC. Notice also that all four smaller triangles have the same area. When the midpoints of each side are connected to make a triangle, the ratio above always holds and also all four smaller triangles will all have the same areas. Explore this!!