Objectives:
1) To learn what, in general, is the slope of a line
2) To learn how to calculate the slope of a line
3) To distinguish between lines with positive, negative, zero, or undefined slopes
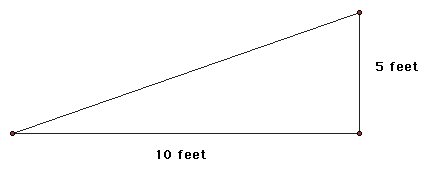
1) Many students will go blank when you ask them what the slope of a line is. This seems odd because most of them will have an idea of what slope means. They know slope of a hill, slope of a ramp, or some other application of slope that they have encountered. The remedy is to use something they are familiar with to introduce slope. Use the slope of a ramp. Provide them with some figure so they can get a visual representation.

What we have here is a ramp with a constant incline, or slope. Ask them to think about what the slope of the ramp is. Let the students throw out several examples. We are not looking for a number answer here just how to describe, in common terminology, what slope is.
2) After some discussion about slope in general, move the students to think about this in a more mathematical way. In the picture above, the slope of the ramp could be thought of in this way: As you go up 5 feet, you are also, simutaneously, going over 10 feet. If you make this into a ratio, you get 5/10 or 1/2. So the slope is 1/2. Does that make sense? Yes, because for every one foot that you are going up, you have to go over 2 feet. This is the typical way of looking at slope as rise over run, rise/run. In this example, you rise 5 feet as you run 10 feet, so your slope, as the rise/run, is 5/10 or 1/2.
Now, let's look at another example. Suppose we had the following graph:
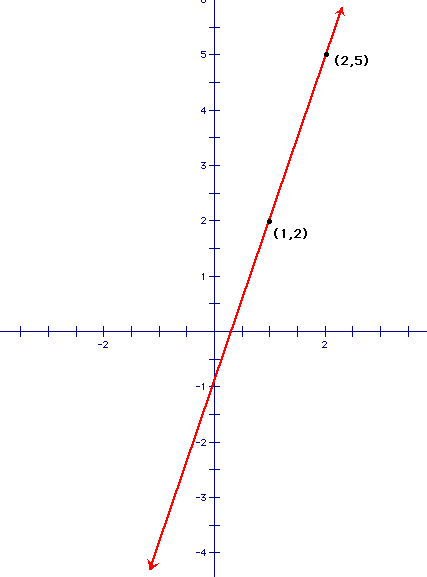
How could we find the slope of this line? Well, slope can also be represented as the change in y divided by the change in x. Another way to say this is delta y/delta x or another way, and the most common is
What this above formula means is that you take your two ordered pairs from your graph. In this case we have (1,2) and (2,5). We know that ordered pairs in general are (x,y). So we designate one point as point 1 and the other as point 2. We do this because our first point will be (x1,y1) and our second point will be (x2, y2). It makes no difference which point you select as point 1 and which one you select as point 2. So, let's choose (1,2) as our first point and (2,5) as our second point. Using the formula for the slope of the line that I gave above, let's find the slope. x1 for us will be 1, x2 will be 2, y1 will be 2, and y2 will be 5.
Using the same rationale from the ramp example, how could we have found the slope? Well, we said that it was the rise over the run. Well, starting at our first point, (1,2) how much did we have to rise to get to the second point? We had to rise 3. How much did we have to run over? Our run was 1. So to find the slope, we would do rise/run which would be 3/1 or 3. So either way we get the same answer for what the slope should be. This is the case each time. No matter which way you choose to find the slope, when done correctly, you will get the same correct answer.
3) In each of the two above examples, each slope was a positive amount. In the ramp example, the slope was 1/2 and in the line example, the slope was 3. Are slopes always positive? No. Slopes can be positive, negative, zero, or even undefined. Think of positive slope as this. If you start at the far left given point and you have to walk up the line to get to the next point, as we did above, then the slope will be positive. If you start at the far left given point and you are walking downhill to the next point, then the slope is negative. An example of a line with a negative slope is below:
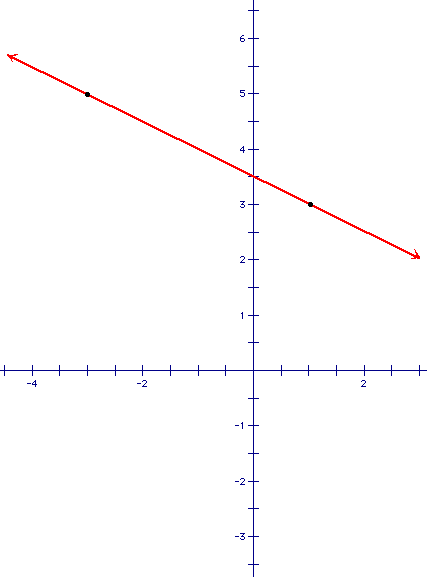
If you start at the point on the left and walk
to the point on the right, you will be walking downhill, therefore,
you can tell immediately that the slope is negative.
What about a line that has zero slope? A line that has zero slope is a horizontal line. Let's look at the line below:
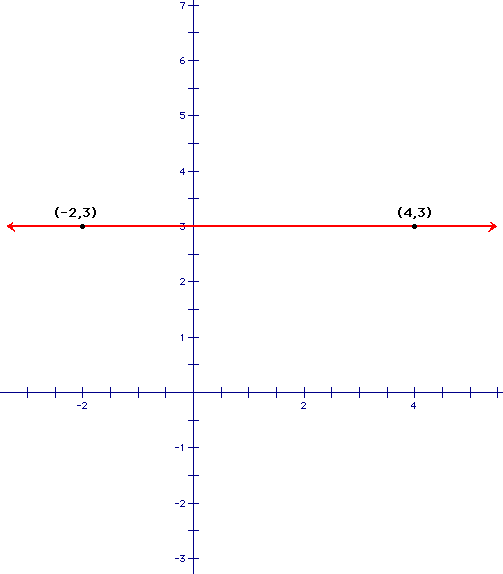
Let's use the rise over run method for calculating the slope. What is the rise, how much do you have to go up or down to get from the point on the left to the point on the right? Well, we find that the rise is 0. How much is the run? In this case, the run is 6. So we have rise/run or 0/6. And we know that 0 divided by any number is 0. Therefore, the slope of this line is 0. Does it matter what the run is? No, because there will still be a 0 in the numerator therefore the slope will still be 0.
What about a line that has undefined slope? Well, it turns out that a line that has undefined slope is a vertical line. Let's look at the one below:
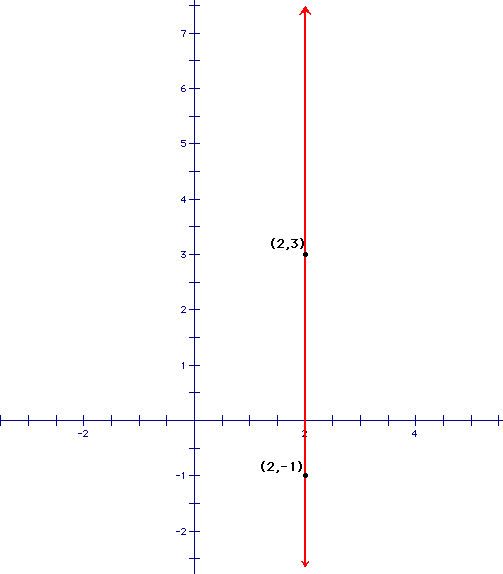
Let's once again use our rise/run method. How much do you have to rise to get from the point on the bottom to the point on the top? We have to rise up 4. How much do we have to run over? We don't have to go over any so our run is 0. Therefore, our rise/run is 4/0. And we know that when there is a 0 in the denominator, then it is undefined. So the slope of this line is undefined. Would it have mattered if the rise had been anything other than 4? No because the denominator would still be 0.
This would be a great time to use a GSP demonstration in your classroom. First, go to graph and show grid. Then plot two points. Choose those two points and go to construct and line. Then, highlight the line and go to measure and slope. The slope will come up and when you move the line around, the slope will change. If you want to move the two points and have the kids find the slope, you can always choose the box that the slope is in and go to display and the hide (make sure that only the slope box is highlighted). If you want to display the slope feature again then go to display and unhide. This is a powerful tool to use in aiding student learning about slope.
Return to Instructional Unit overview