

The objective of this assignment was to investigate two linear functions whose product is tangent to both functions.
I started with, what I feel are the two most logical equations to begin with:
Therefore, the product of these two linear functions and the graph of these functions are:
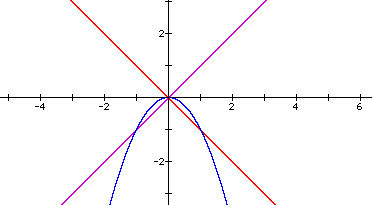
The product, h(x), is obviously not tangent to both functions. Therefore, I tried the following other functions and their products. The graphs immediately follow.
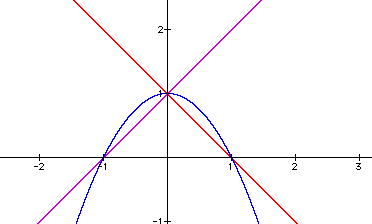
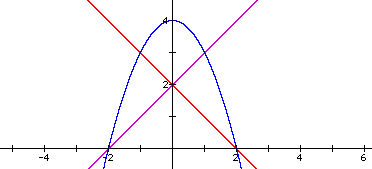
It definitely seems that I may have taken the wrong approach by adding 1 to x and then 2 to x. Therefore, I decided that I would go the other direction and try adding 1/2 to x.
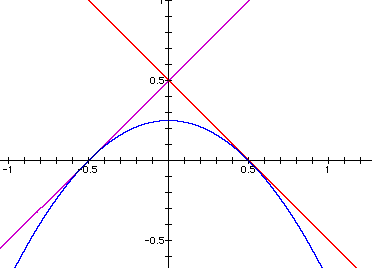
This appears to be the combination of functions that I was looking for. The product function appears to be tangent to f(x) at -1/2. Because -1/2 satisfies both f(x) and h(x), we know that the two functions intersect at that point. By taking the derivative of both functions, we can see what the slopes are at a given point. The f'(x) is 1 and h'(x) is -2x. Since we know where the functions intersect, at -1/2, substituting -1/2 for x in f'(x) and h'(x) gives us the slope of the original functions at their intersection point. If the two slopes are the same then the graphs of the original functions will tangent at the intersection point, -1/2. Since there is no x in f'(x), then the slope is just 1; h'(x) is -2(-1/2) which is 1. Therefore, the graph of the product is tangent to the function. A similar argument can be made for the product function and g(x). The graphs of these two functions are tangent at 1/2.
Therefore, I have found two functions whose
product is tangent to the functions.