

For this assignment, I will look at various triangles and their circumcenters. The circumcenter of a triangle is the point in the plane equidistant from the three vertices of the triangle. Since a point equidistant from two points lies on the perpendicular bisector of the segment determined by the two points, C is on the perpendicular bisector of each side of the triangle. The perpendicular bisector of a side goes through the midpoint of the side and forms a right angle to side of the triangle. To find the circumcenter of a triangle, you first need to find the midpoints of each side of the triangle. This step is performed below.

As is probably evident, D, E, and F are the midpoints of the three segments of the triangle. The next step in finding the circumcenter of triangle RST is to construct the perpendicular bisectors of each side of the triangle. This step is done below.
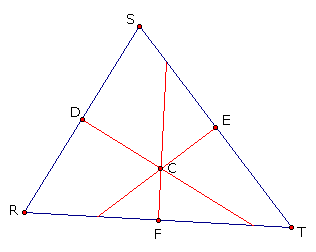
As you can see, these perpendicular bisectors are concurrent at C, the circumcenter. We have already stated that C is equidistant from R, S, and T, the three vertices of the triangle. Because this is so, if a circle is constructed with center C and radius of measure CS, all three vertices will be points on the circle. This cirlce is the circumcircle and is shown below.
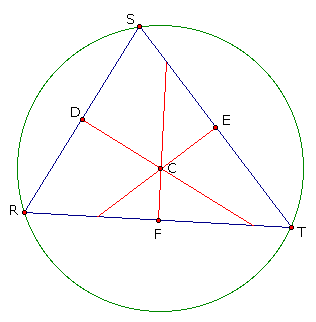
To explore the circumcenters of other shapes of triangles using GSP 4.00, click here. Notice that the circumcenter for an obtuse triangle lies outside the triangle and that the circumcenter is at the midpoint of the hypotenuse for a right triangle.