

For this assignment, we looked at altitudes, orthocenters, circumcenters and circumcirlces. For the first part, we did the following items using GSP:
1. Construct any triangle ABC.
2. Construct the Orthocenter H of triangle ABC.
3. Construct the Orthocenter of triangle HBC.
4. Construct the Orthocenter of triangle HAB.
5. Construct the Orthocenter of triangle HAC.
6. Construct the Circumcircles of triangles ABC, HBC, HAB, and HAC.
The construction should look something like the following:
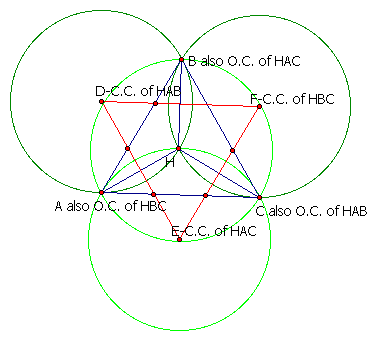
In the construction, C.C. stands for circumcenter and O.C. stands for orthocenter.
As you can see, each vertex of the original triangle ABC is also an orthocenter for one of the smaller triangles formed by two of the vertices of the original triangle and H, the orthocenter of the original triangle.
I made two conjectures about this construction. First, it appears that the original triangle, ABC, and the triangle formed when the three circumcenters are connected, DEF, have the same area. The following is not a proof, but it seems to support this conjecture. Explore moving these triangles around,by moving either point A,B, or C, and notice that the areas remain the same.
Secondly, it also appears that the areas of the 4 circles that are in the construction are also always equal. Again, the following exploration is not a proof, but notice that as you move A,B, or C, the areas for the circles are the same.
For the second part of the assignment I looked at the following problem:
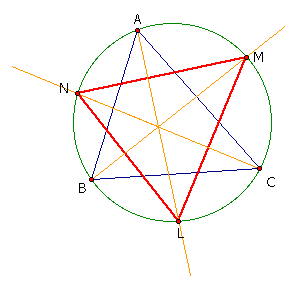
The internal angle bisectors of triangle ABC are extended to meet the circumcircle at points L,M, and N, respectively. Find the angles of triangle LMN in terms of the angles A, B, and C. Does your result hold only for acute triangles?
Here is what the construction should look like:
Below is the construction with the angles of LMN stated in terms of the angles of ABC.
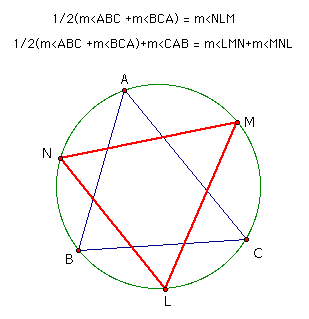
In the following exploration, notice that this seems to hold true for any shape of triangle. You can change the shape of the triangle by moving points A, B, and C.
As you can see, this result held for any shape of triangle.