

For this assignment, we were to explore parametric equations. A parametric curve in the plane is a pair of functions
where the two continuous functions define ordered pairs (x,y). The two equations are usually called the parametric equations of a curve. The extent of the curve will depend on the range of t and for this assignment, the range of t was limited to 0...6.28(2*Pi). In many applications, we think of x and y "varying with time t" or the angle of rotation that some line makes from an initial location.
For this assigment I will look at the following equations
and how to change these equations to obtain and explore other graphs.
When the above two functions are graphed, the result is

As you can see, the curve that results is a circle. What would happen if I made the equations
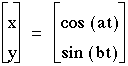
What would the graph of the following equations look like?

Well, these equations produced the same graph as above. So, the next thing I thought about trying was the following equations

The graph was the following

Seeing the graph that was produced from these equations, I wondered what would happen if the following equations were graphed

The graph of the above parametric equations is

Explore further what would happen when one of these values is changed while the other value is kept constant. In the following exploration, b is kept constant at 1 while a ranges from 0 to 7. Now explore what happens when a is kept constant at 1 and b ranges from 0 to 7.
Now, let's see what would happen if we explored the following equations

I first looked at the graphs for values of a=1,2,3 and b=1,2,3. When these are graphed together, the following graph is produced

Unlike before, when the values of a and b are the same, different graphs are formed. What happens when the values for a and b are not the same? Watch how the graph changes as a is kept constant and b is ranged from 0 to 5 and also as b is kept constant and a is ranged from 0 to 5.
Lastly let's look at what some graphs of the following functions would look like

One example is looking at the graph when a=3, b=4.5, c=3, and d=5. It turns out that this is similar to the shape of the ball that is used in my favorite sport...
