

This assignment looks at polar equations. For this assignment, I will investigate the equation
and I will look at three aspects of this equation.
These are: 1)When a and b are equal and k is an integer(n-leaf
rose); 2)compare the above equation with the equation ![]() for various values of k; 3) When cos is replaced with sin.
for various values of k; 3) When cos is replaced with sin.
Before we look at these three aspects, let's look at the graph of
when a,b, and k=1.
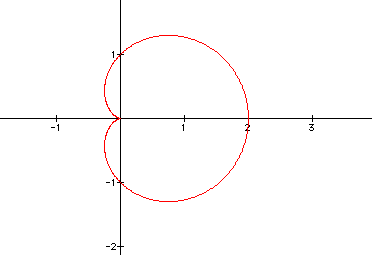
Now, we we'll look at the first part of the assignment. The original equation above yields what is often known as the n-leaf rose. It could be called the k-leaf rose because in our equation, the value for k determines how many leaves will be on the graph. The following graphs show this relationship. The values of a and b are 1 for each equation and the values of k are 3, 4, 5 respectively.
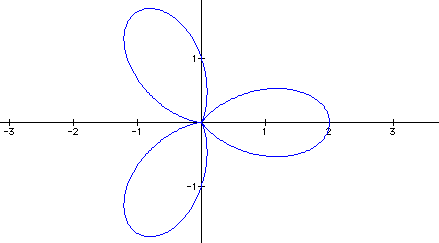
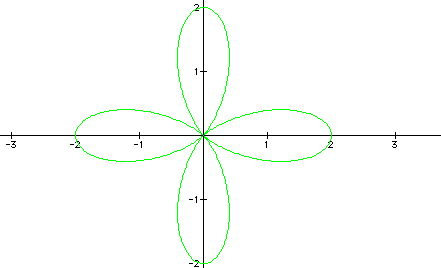
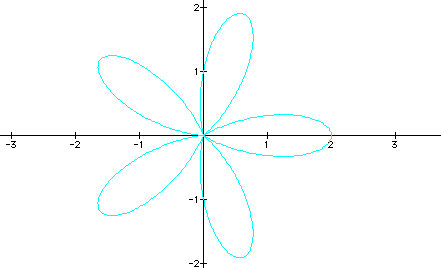
As you can see, the leaves of the graph equal the value of k.
For the second part of this assignment, we will compare our original equation
with the equation
for various k values. When k is 0, both equations yield a circle with the circle of the second equation inside the first equations circle.
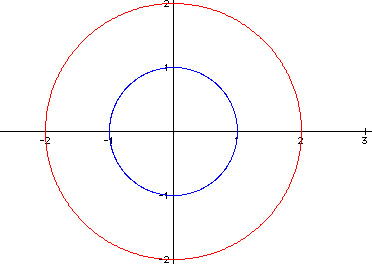
When k is 1, both equations have 1 leaf.
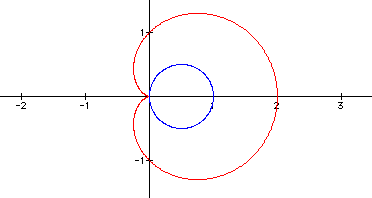
When k is 2, there are 2 leaves for the original equation, which we know from above, and there are 4 leaves for the second equation with 2 leaves inside the two leaves of the first equation; the graph is below.
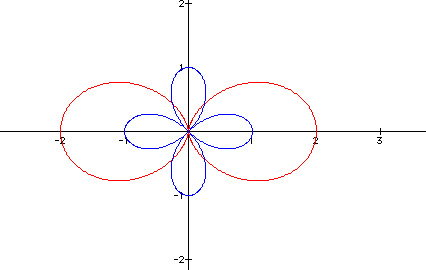
When k is 3, each graph has 3 leaves with the leaves of the second equation inside the 3 leaves of the first equation; the graph is below.
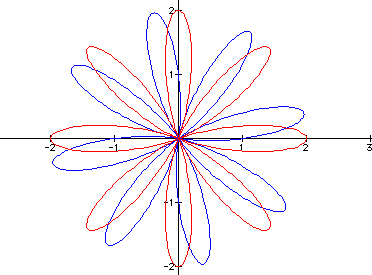
These patterns remain the same; for odd values of k, both graphs have equal number of leaves with those of the second equation completely inside the first, for even values of k, the second graph has 2k leaves and the first just k leaves. Take a look at the graphs when k=5, k=8, also look at the sun and a sand dollar.
For the last part of the assignment, I will
look at what happens when ![]()
is compared to ![]() . The
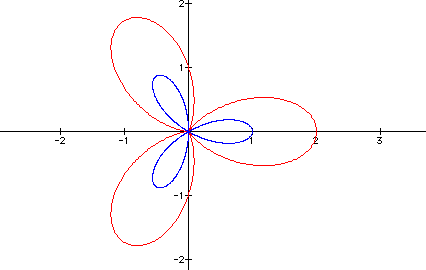
graphs of these two are below. The value for a and b is 1 and
the value of k is 3. The cosine graph is in red and the sine graph
is in blue.
. The
graphs of these two are below. The value for a and b is 1 and
the value of k is 3. The cosine graph is in red and the sine graph
is in blue.
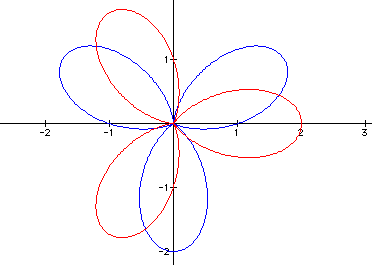
As you can see, the graphs are the same with a translation.