This assignment allows us to explore some aspects of spreadsheet programs. I chose to construct a graph of any function y = f(x) by generating a table of values with the x values in one column and the y values in another. The spreadsheet program that I used was Excel. I chose a random f(x). The function I chose first was f(x) = (x/2)^2. I chose to look at this function for x values ranging from -10 to 10. The x and y values are below.
| X | Y1 |
| -10 | 25 |
| -9 | 20.25 |
| -8 | 16 |
| -7 | 12.25 |
| -6 | 9 |
| -5 | 6.25 |
| -4 | 4 |
| -3 | 2.25 |
| -2 | 1 |
| -1 | 0.25 |
| 0 | 0 |
| 1 | 0.25 |
| 2 | 1 |
| 3 | 2.25 |
| 4 | 4 |
| 5 | 6.25 |
| 6 | 9 |
| 7 | 12.25 |
| 8 | 16 |
| 9 | 20.25 |
| 10 | 25 |
Intuition told me that this should be a parabola and the x and y values seem to support this. The graph should tell us more.
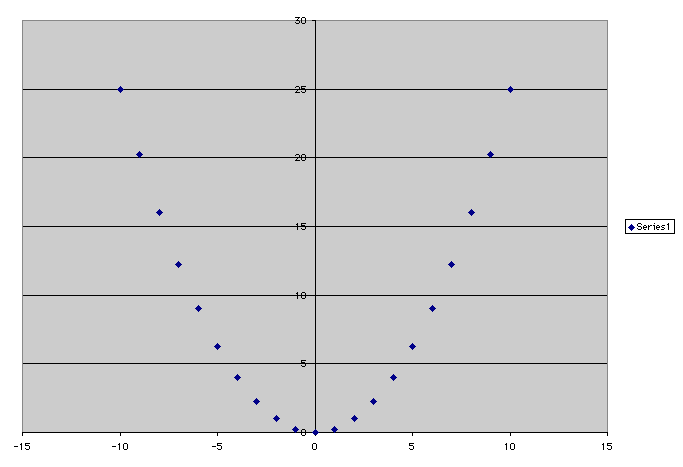
The graph seems to further support the claim that this is a parabola, and indeed it is.
The second function that I looked at was -(x/2)^2+x-1. The x and y values are below.
| X | Y2 |
| -10 | -36 |
| -9 | -30.25 |
| -8 | -25 |
| -7 | -20.25 |
| -6 | -16 |
| -5 | -12.25 |
| -4 | -9 |
| -3 | -6.25 |
| -2 | -4 |
| -1 | -2.25 |
| 0 | -1 |
| 1 | -0.25 |
| 2 | 0 |
| 3 | -0.25 |
| 4 | -1 |
| 5 | -2.25 |
| 6 | -4 |
| 7 | -6.25 |
| 8 | -9 |
| 9 | -12.25 |
| 10 | -16 |
This, too, should be a parabola. The graph is below.
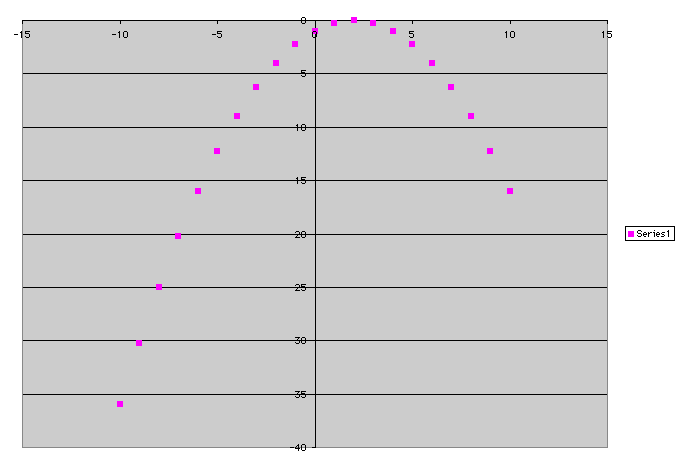
Indeed, this is also a parabola.
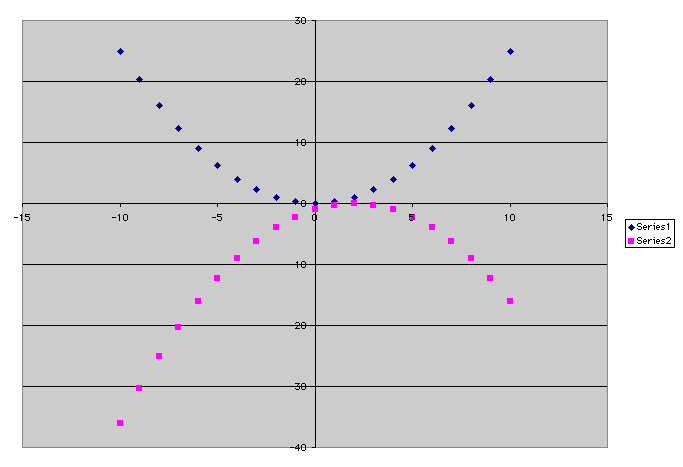
The last thing that I did was put these x and y values together and graphed the functions together. Below are the x and y values.
| X | Y1 | Y2 |
| -10 | 25 | -36 |
| -9 | 20.25 | -30.25 |
| -8 | 16 | -25 |
| -7 | 12.25 | -20.25 |
| -6 | 9 | -16 |
| -5 | 6.25 | -12.25 |
| -4 | 4 | -9 |
| -3 | 2.25 | -6.25 |
| -2 | 1 | -4 |
| -1 | 0.25 | -2.25 |
| 0 | 0 | -1 |
| 1 | 0.25 | -0.25 |
| 2 | 1 | 0 |
| 3 | 2.25 | -0.25 |
| 4 | 4 | -1 |
| 5 | 6.25 | -2.25 |
| 6 | 9 | -4 |
| 7 | 12.25 | -6.25 |
| 8 | 16 | -9 |
| 9 | 20.25 | -12.25 |
| 10 | 25 | -16 |
And the two functions graphed together are below.