

Take any quadrangle. Construct a quadrangle connecting the four midpoints of the sides. This is called the Medial Quadrangle.
Click Here for GSP file.
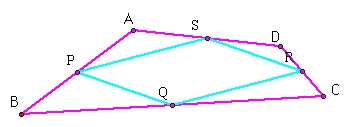
It is parallelogram and one-two of its area (Click Here for GSP file ). Prove it? Click Here for proof.
1. Construct the medial quadrangle of square. What is this figure? Prove? Click here for GSP file.
2. Construct the medial quadrangle of rectangle. What is this figure? Prove? Click here for GSP file.
3. Construct the medial quadrangle of diamond.What is this figure? Prove? Click here for GSP file.
4. Construct original triangle to be reqtangle medial rectangle. Click here is GSP file.
5. Construct original triangle to be diamond medial rectangle. Click here is GSP file.
Given four points A,B,C,D on 3D space. Connect the midpoints of segments AB, BC, CD, DA. What kind of figure is this?
Proof?
Construct Quadrangle ABCD , and six lines AB,AC,AD,BC,BD,CD(Connect all vertexes). The intersections of AB and CB mark E, and intersection of AD,BC mark F. Construct line EF. Intersections of EF and AC, BD mark G,H. What is the rerationship of EG:GF and EH:HF? Click here for GSP file.
1. Given two segment AB,CD and two points E,F on the each segments. Construct midpoint M of segment EF. What is the locus of M when E,F moving on the segments? Click here for GSP file.
2. Given a segment AB , circle c1 , and two points C,D on the each object. Construct midpoint M of segment CD. What is the locus of M when C,D moving on the object? Click here for GSP file.
3. Given a two circles c1,c2, and two points A,B on the each circles. Construct midpoint M of segment AB. What is the locus of M when A,B moving on the circles? Click here for GSP file.
Note:
Subsumption of Parallelogram is welknown teaching material using dynamic geometry software in Japan. There are many practical lessons and studies using this material.
There are practical study of Quadrangle on 3D Space using model of 3D quadrangle this year.
The first problem of Similar Tranceformation is showed me from Dr.Fujii ( Tokyo Gakugei University)
Click here for paper of my presentation . Microsoft Word file 96K.