The graph of is below:

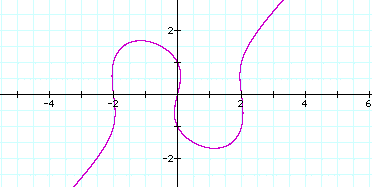
Let's try to replace the 4 by 5 , 3 , 2 , 1 , 1.1 , 0.9 , and observed the graphs on the same axes as following:

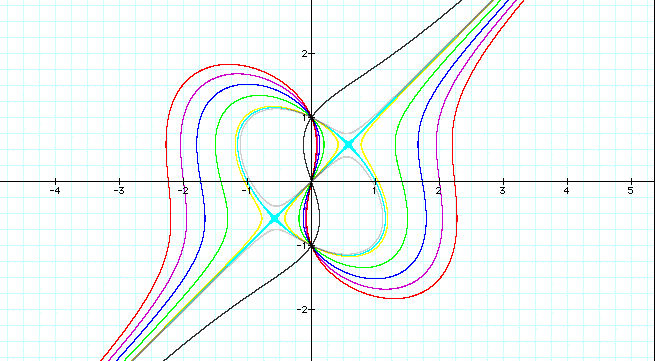
See the graph, replaced bigger number, the graph gradually expands. There are two similarity of the all graphs by this observation. One is there are the three common points, (0,-1),(0,0),(0,1). The other is these graphs are central symmetry with the center point of the origin . While we notice that the light blue graph differs from others, and change the shapes from before this point to after.

Go on the observation to see graph of .

Observation of -15 < n < 15 graphs here.

When n>1 the graph's shape and the original one are the same.

When n=1 the graph is a line with a ellipse.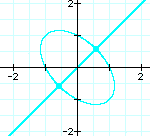

When n<1 the graph have no minimum and no maxmum.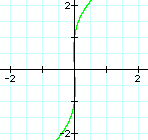

Why does the graph of pass the three points (0,1),(0,0),(0,-1)? Is it true, when n is any number,the graph of the equation pass the three points? The similarity of these three points is x=0. So let's try to substitute x=0 for this equation. And find the intersections of this equaition and x=0 by algebraic approach.

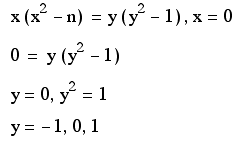
This means when n is any number the graph of this equation have the three common points, (-1,0),(0,0),(0,1).

The central point of the symmetry is the origin.So let's try to explore using the line of y=ax as following:

For example:

Graph following equations on the same axes: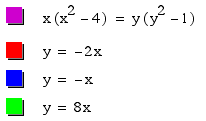

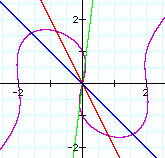
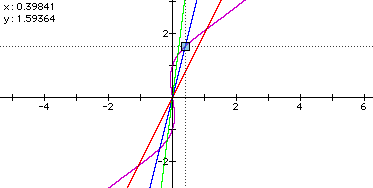
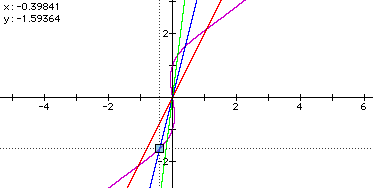
Then, we can oveserve the coordinate of the intersection points of and y = ax . For example:

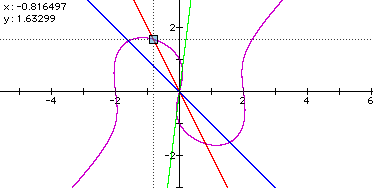
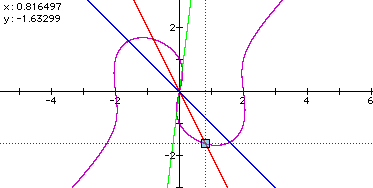
Can you notice the signs of coordinate of intersections are opposite with the same absolute number? It means that the each intersections are the position of the central symmetry with the center point of the origin. Let's try another graphs. For example or .

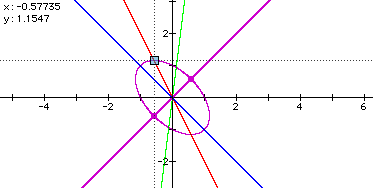
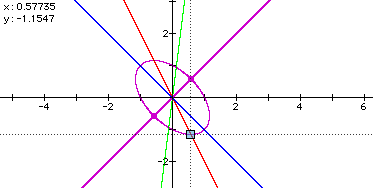
with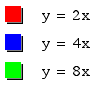

Is it true, when a is any munber, the graph of is the center symmetry with the central point of origin? We can solve this problem as searching intersections of the following equations by argebrical approach.:

and y = ax

Acoording to the above exproing , these equations don't have three intersections anytime. How many intersections do the equations have with how range of a? What are the coordinates then?

First, let's try to solve the following equations : and y = ax. Here is algebraic approach.

Next, and y = ax. Here is algebraic approach.

Now focus on the n=1 graph.

Why is the graph a line with a ellipse on this point? Development the equation of as following:

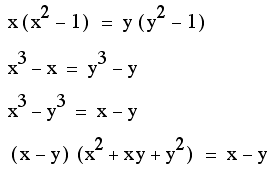
When x=y , the equation anytime conslude.

When x not = y , we can devide both side of the equation by (x-y), then .

Therefore the graph of the equation is constructed by line of and .

The graph of is below:

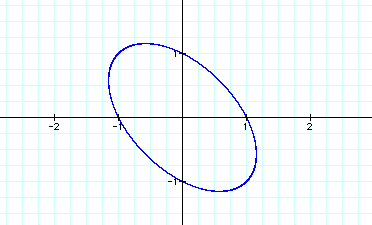
By the way, is it true, the graph of the equations of is ellipse? Here is argebraic approach.

What is shape of the graph of? Is the same graph of ?

Let's try to replace n for -3,-2,0,0.5,2,6 as following:

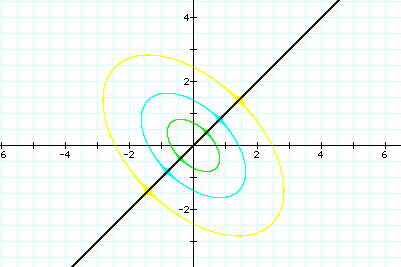
All graphs through the line of y=x, but as n<0 , ellipse disappear.

Observe the graph of .

If we think about plane of z=n,we observe the graph of from 3D space.

Return