

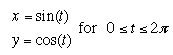 is as following;
is as following;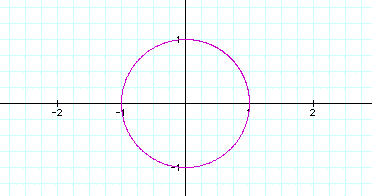
Let's try to change the equations to explore other graphs!
Let's try to investigate the equations 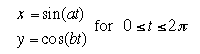 for various a and b !
for various a and b !
When a=1 and b=1, then the graph of the equations and above graph are same shape (circle) .
Let's try to change the a for various number in the case of b (b=1) is fixed !
a=2.b=1
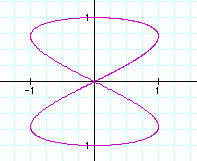
a=3,b=1
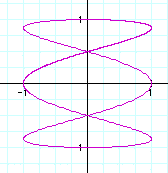
a=4,b=1
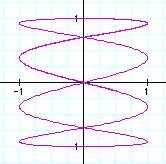
It seems the number of a concern with the nimber of rings. How about decimal?
a=2.1,b=1
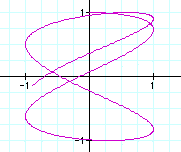
a=2.3 , b=1
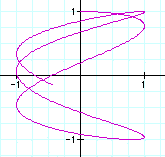
a=2.5 , b=1
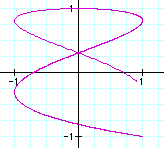
a=2.9 , b=1
Click here for
movie file of In the case of![]() .
.
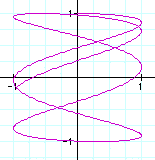
Let's try to change the b for various number in the case of a (a=1) is fixed !
a=1, b=2
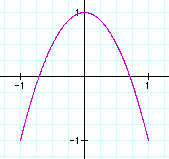
a=1 , b=3
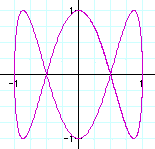
a=1, b=4
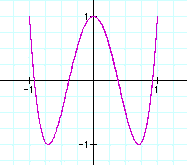
a=1, b=5
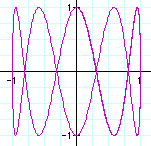
a=1,b=6
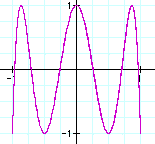
Concerning with the number of rings is when b is odd number. When b is even number, it seems the number of b concern with the number of concave. It seems a-1.
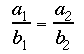
In the case of ![]() , let's
try to conparasol two equations
, let's
try to conparasol two equations 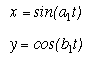 and
and![]() !
!
a=1 ,b=3
Look at above graph !
a=2 ,b=6
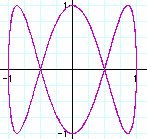
a=4, b=12
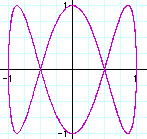
a=5, b=4
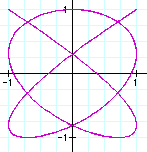
a=10, b=8
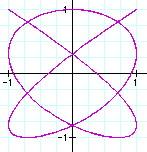
It seems that the graphs are same in the case
of ![]() .
.