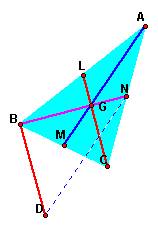
The triangle ABC is
original.The points of L,M,N are midpoins and AM,BN and CL are
medians.
When we translate the median LC parallel with troughing the point of B and mark the end of the parallel segment with D, prove the follow.
1. Prove the quadrangle BDCL is parallelism.
The sides of BD and LC are parallel and have same length. So the quadrangle BDCL is paralleism.
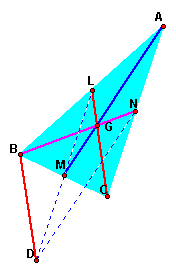
2. Prove the length of the segment ND and the median AM are same.
Now Focus on the quadrangle MDNA. Because the quadrangle BDCL is parallelism, diagonal lines intersect on the midpoint each lines. So the point of M is intersection of diagonal lines. The point L,M and N are midpoints the sides of the original triangle,so LD//AC and LM=MD=AN=NC.Because of MD//AM and MD=AN, the quadrangle MDNA is paralleism, so ND=AM and the three sides of triangle BDN have the length of three medians from original triangle .