

Let's examine the following equation:
The graph of this equation looks like this:
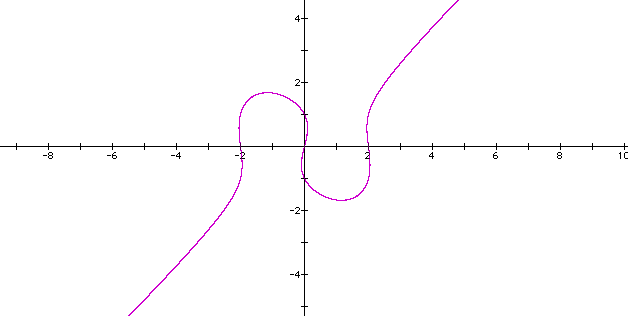
If we replace the 4 with other numbers, and let's see what happens.
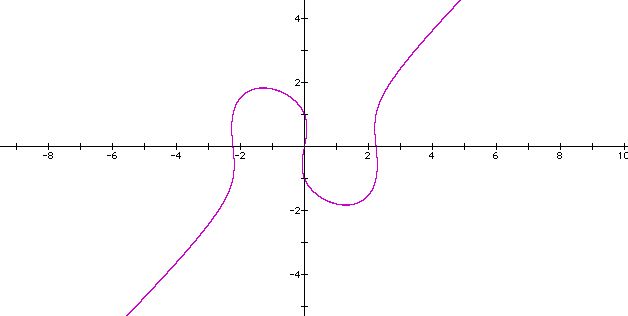
The graph expands horizontally just slightly.
Let's try replacing the original 4 with 3:
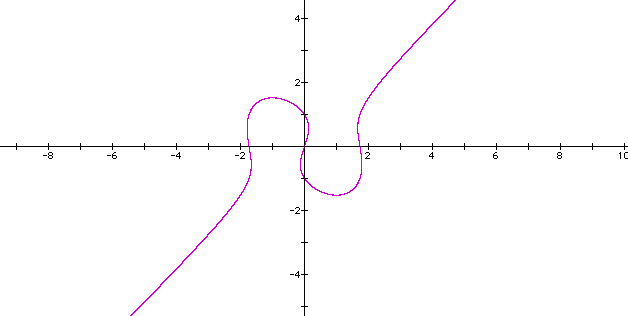
As expected, the graph seems so retract horizontally.
What if we replace the original 4 with 1?
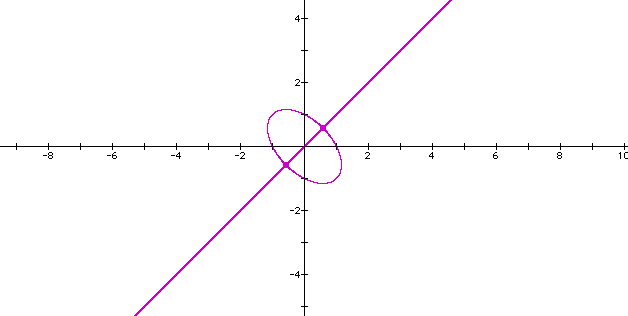
This is a surprise. The graph forms an ellipse still centered at (0,0), with a diagonal line through it.
Did this occur only when the 4 is replaced with 1? let's try replacing the original 4 with 1.1.
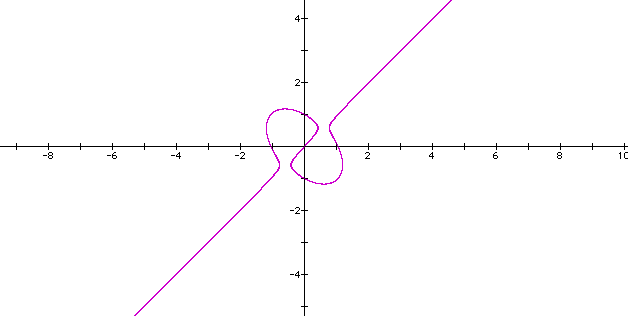
The graph appears to approach our original graph. The ellipse has not been formed . We can see that the graph is appraoching an ellipse at its center.
The center of the graph has refected 180 degrees while still approaching the assymptotes. The center has also become more rounded.
If we replace the original 4 with 0.9, will the graph look more like our original graph or will it approach as ellipse?
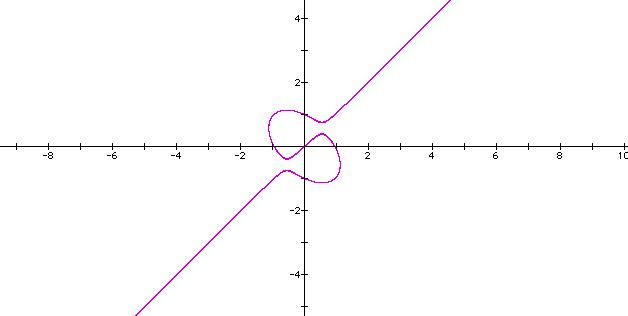
The graph seems to be approaching an ellipse .
What if we replace the original 4 with a -3, will it approach our original graph?
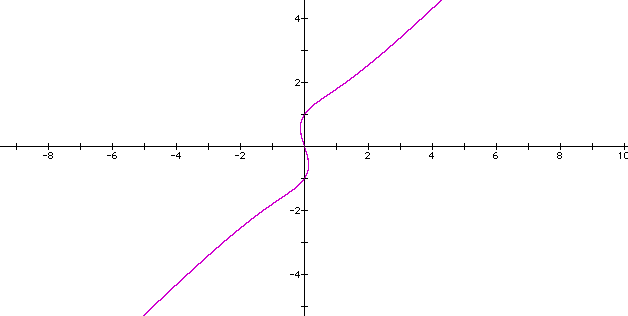
This graph does not resemble our original graph.
Let's look at this graph with our original graph, so we can make comparisons.
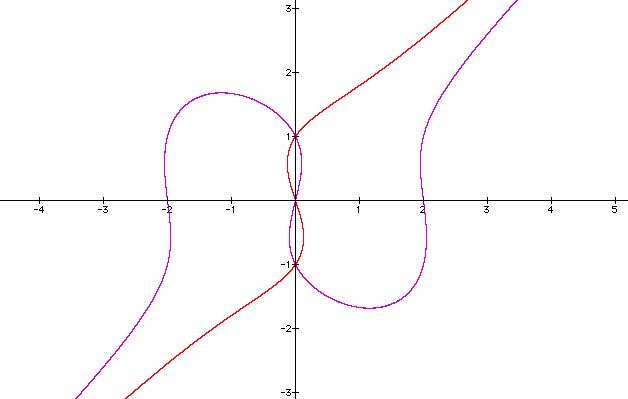
The graph appears to have refected on the y-axis, and retracted horizontally.
All of these graphs are centered at (0,0), and the legs are all approaching the assymptote.
Let's see what happens if we add a constant to one side of our original equation.
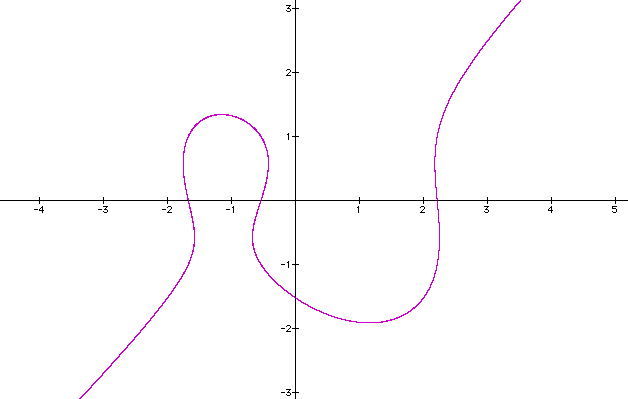
The left side of the graph is retracting horizontally, the right side of the graph is expanding horizontally, and it is difficult to find the center. The center must be around (-0.75, -0.75).
Let's try some different constants to see what happens.
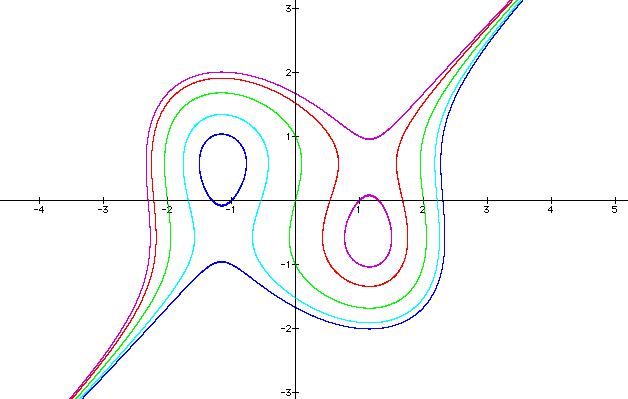
As we can see the graph forms an enclosed shape when the constant is 3 and when it is -3. The legs continue to appraoch some assymptote.
Let's try graphing the following equation.

The graph becomes 3-dimensional.
Let's replace the 4 with -3 and see what happens.
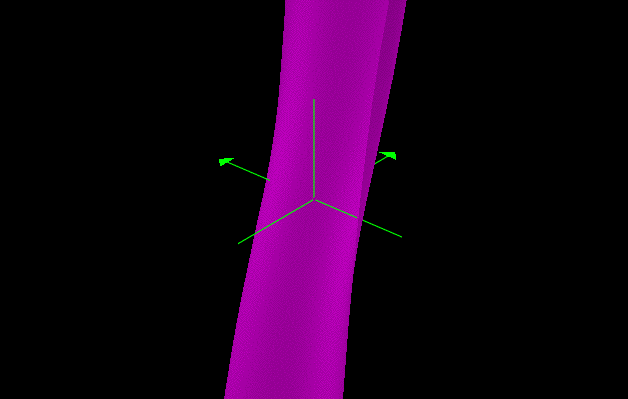
The graph approaches a plane through the x-axis.