

Let's examine some parametric equations.
Explore the graph
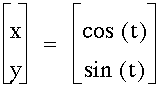
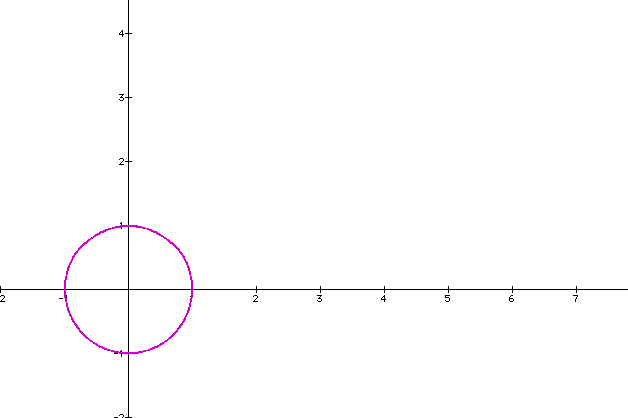
This graph appears to form a circle with center at (0,0) and a radius of 1.
How would you change the equations to explore it further?
What about the parametric equations
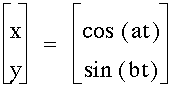

This is the same graph as before, because a and b are 1.
Let's change a and b to investigate it further.
Let's change a to 3.
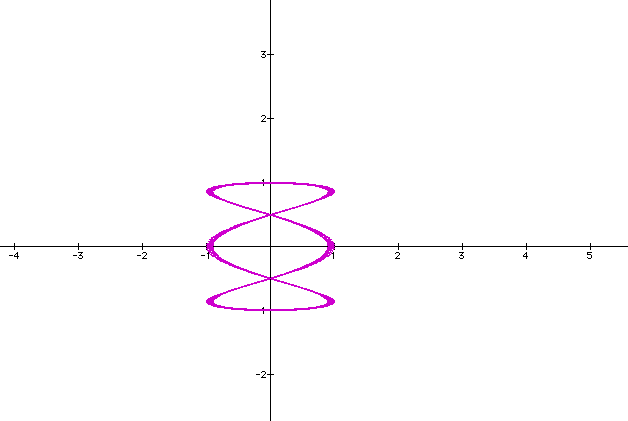
Our graph has changed drastically. We now have 4 y-intercepts.
Let's change b to 3.
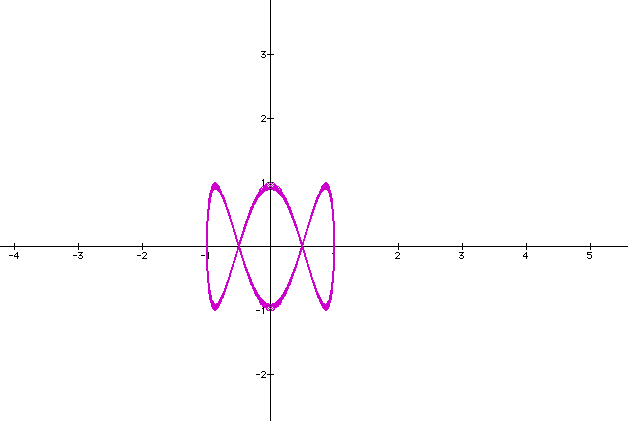
With a=1, our graph is rotated 90 degrees. We now have 4 x-intercepts.
Let's change a and b to 3 to see how our graph changes.

It appears as though we have several circles centered at (0,0). I would guess that we have 4 intercepts on each axis that are connected on this graph.
It appears that the curve changes drastically as a and b are changed.
What if the equations look like
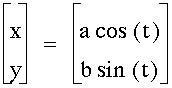
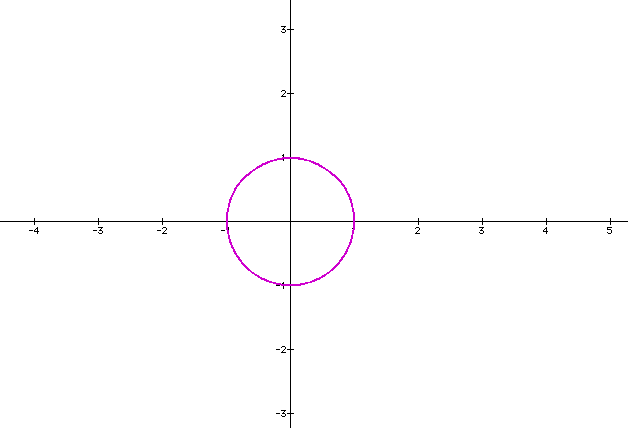
Since a and b are 1, we get our original graph.
Let's change a and b to investigate.
Let's change a to 3 and see how the graph changes.
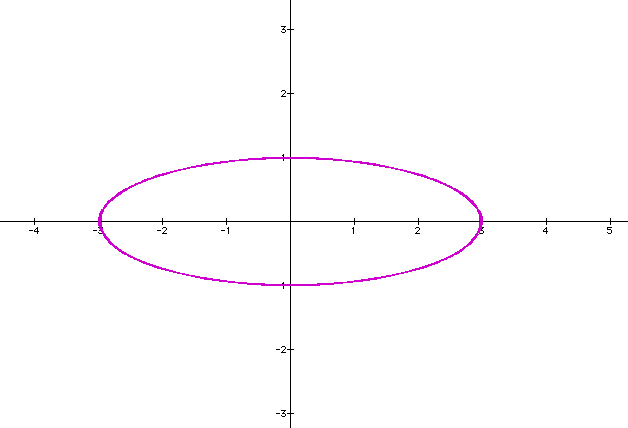
Our graph is an ellipse centered at (0,0) with x-intercepts at 3 and -3.
If we let a=1 and b=3, I would guess that our ellipse will be rotated 90 degrees. Let's see.
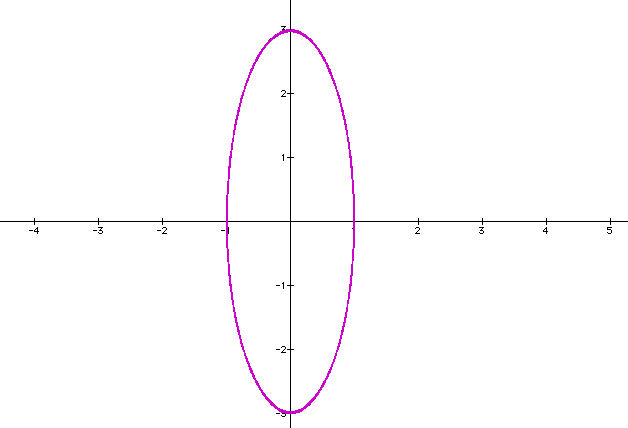
My prediction was correct. Our ellipse rotated 90 degrees and is still centered as (0,0) with y-intercepts at 3 and -3.
What if we let a=3 and b=3?
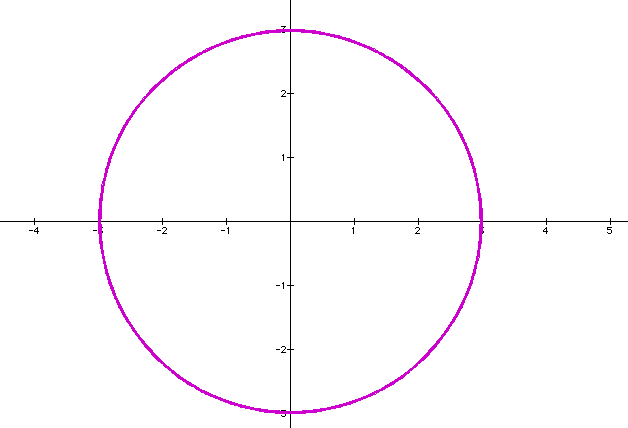
We can see that our graph is a circle again. The center remains at (0,0) whenever a and b change. This circle has y-intercepts and x-intercepts at 3 and -3.
Once again a and b play an important roll in these equations. The curves move and change shape as a and b change. And a and b determine the y and x-intercepts.