

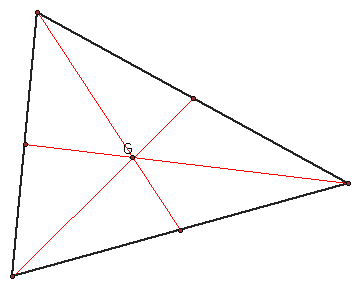
The centroid of a triangle is the intersection of the three medians.
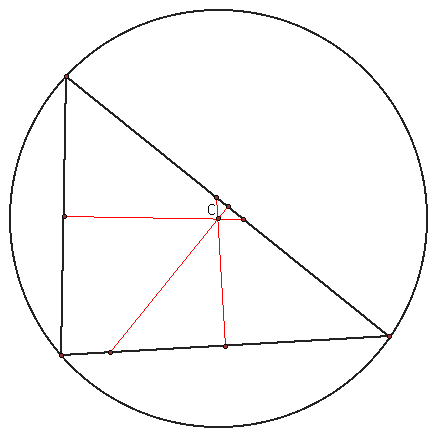
The circumcenter of a triangle is the point in the plane equidistant from the three vertices of a triangle. Since a point equidistant from two points lies on the perpendicular bisector of the segment determined by the two points, C is on the perpendicular bisector of each side of the triangle.
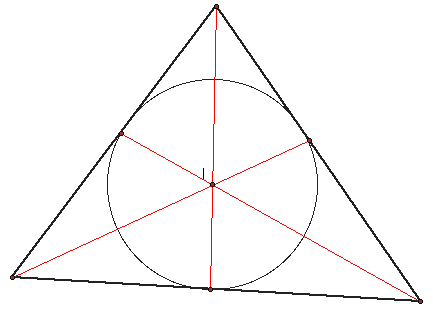
The incenter of a triangle is a point equidistant from all three sides of the triangle.
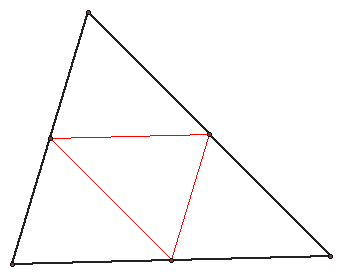
The medial triangle is a triangle constructed from the feet of the medians of the triangle.
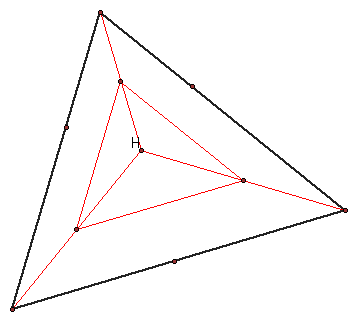
The mid-segment triangle is a triangle constructed from the midpoints of the segments connecting the orthocenter to the three vertices.
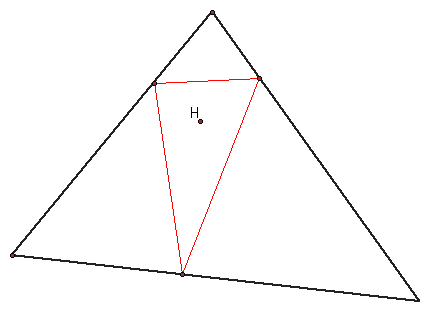
The orthic triangle is a triangle that is constructed by connecting the feet of the perpendicular bisectors of a triangle.
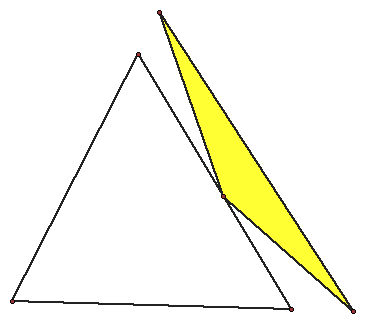
The pedal triangle is a triangle constructed by choosing an arbitrary point in the plane. Next three lines are constructed from the point that are perpendicular to each side of the triangle. Segments are drawn connecting the three intersections of the lines to create the pedal triangle.
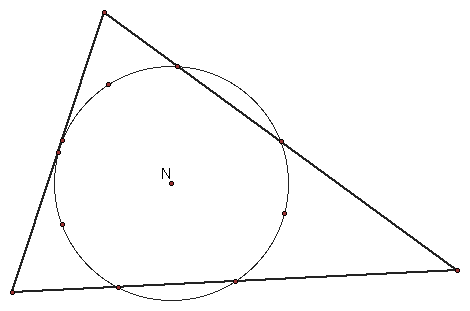
The nine point circle is constructed by finding the 3 vertices of the orthic triangle, the 3 midpoints of the sides of the original triangle, and the 3 feet of the altitudes. The center of the triangle is found, and then the nine point circle is constructed through the nine points and around the center.
To trisect a line segment, first construct a line segment. Find the midpoint and then construct a circle with the endpoint as the center and the length from the midpoint to the end as the radius. Do this at both endpoints.Next construct a segment that goes from one endpoint to the intersection of the circle and the line of the opposite side of the segment. Where the small circle and large circle intersect, construct a perpendicular line through the segment. The perpendicular line divides the segment into one third. Repeat on the other side of the segment to find the other third.
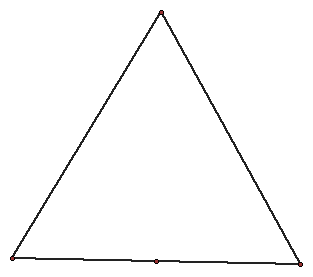
This equilateral triangle was constructed by constructing a line segment. Next a circle was constrcuted on on end with the segment as the radius. Since an equilateral triangle has three equal sides, the other two sides have to be the length of the segment. Another circle was constructed at the other end of the line segment with the segment as the radius. Where the two circles intersect is a vertex. A segment was constructed connecting the intesection to the two endpoints forming an equilateral triangle.

This square was constructed from one given side. First a line segment was constructed to form the given side. Next, a circle was constructed at each endpoint with the line segment as the radius. A perpendicular line was constructed through each enpoint to locate the other two vertices. The vertices were connected to form a square.
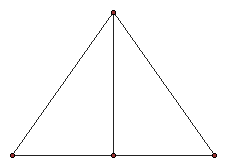
An isosceles triangle has two sides of equal length. Given the base, the midpoint needs to be located, and a perpendicular line constructed through the midpoint. Next the length of the altitude needs to be constructed on the perpendicular line from the midpoint. The other end of the altitude is a vertex of the triangle. Contruct a line segment from the end of the altitude to the endpoints of the base to construct an isosceles triangle.
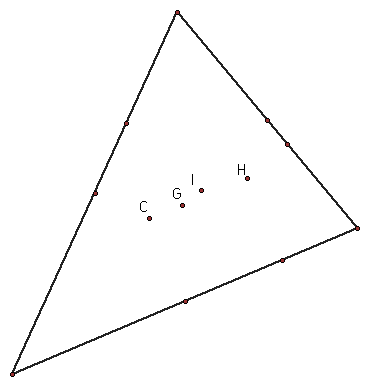
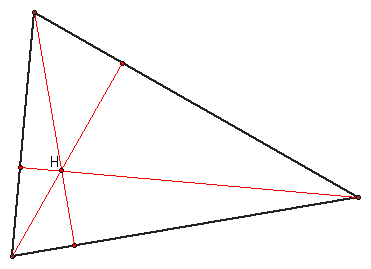
The triangle centers are the centroid (G), the incenter(I), the circumcenter (C), and the orthocenter, (H).
Dividing a segent into the Golden Ratio

A segment divided into the Golden Ratio is constructed by taking its midpoint and constructing a perpendicular line at one of the endpoints. Next a circle is constructed with 1/2 the length of the segment as the radius. Next, a line is constructed from the intersection of the perpendicular line and circle to the end of the segment forming a triangle. A circle is constrcuted at the other endpoint, and where it intersects the original segment divides the segment into the Golden Ratio.
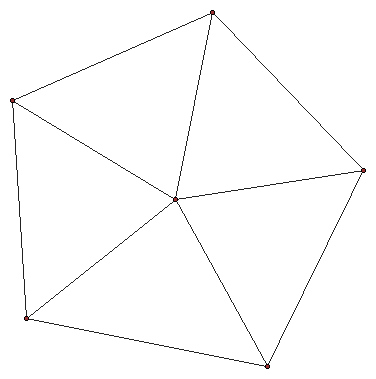
This is a regular pentagon constructed from the radius. Given a line segment (the length of the radius), we know that the center angles of the pentagon are 72 degrees. So, if we rotate the segment 72 degrees and connect the endpoints 5 times we get a pentagon.
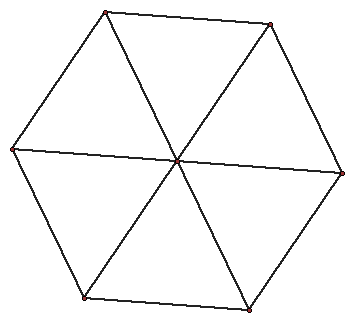
First a segment is conctructed. Next, a circle is constructed at each endpoint with the segment as the radius. Where the two circles intersected, another circle was constructed with the segment as a radius, where the new circle intersected the other circles is where to find the vertices of the octogon. This process is repeated until the octogon is formed.
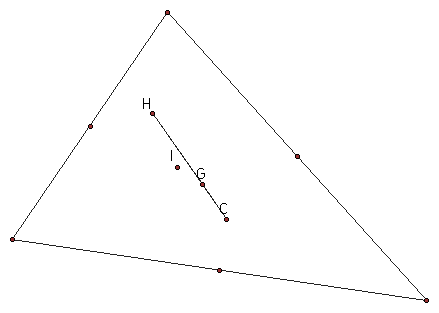
The Euler line is the line connecting the orthocenter, centroid, and circumcenter of the triangle.