

Construct a triangle ABC. Then construct a pedal triangle RST.
(Need help constructing a pedal triangle.)
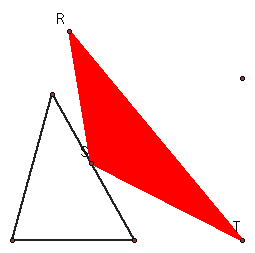
Script for pedal triangle construction.
What if pedal point (p) is the centroid of triangle ABC?
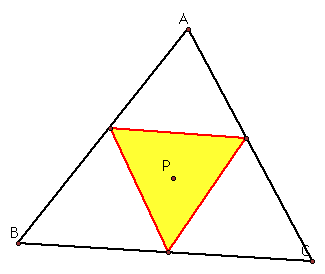
To move the triangle ABC or the pedal point to see how the pedal triangle changes click here.
We can see that the pedal triangle stays inside triangle ABC.
What if the pedal point (p) is the incenter of triangle ABC?
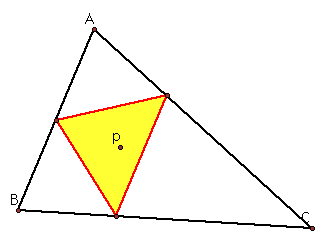
To see how the pedal triangle changes as you move triangle ABC click here.
We can see that the pedal triangle stays inside triangle ABC as triangle ABC moves.
What if the pedal point (p) is the orthocenter?
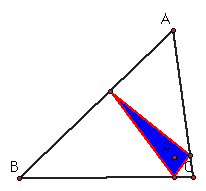
To see how the pedal triangle moves as you change triangle ABC click here.
We can see that the orthocenter moves outside triangle ABC, but the pedal triangle disappears. When the orthocenter is inside triangle ABC, the pedal triangle moves inside.
What if pedal point (p) is the circumcenter?
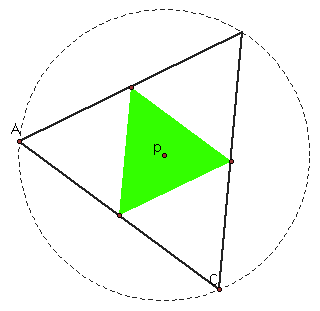
To move triangle ABC to see how the pedal triangle changes click here.
We can see that the pedal triangle is only present inside triangle ABC. And triangle ABC disappears often.
What if the pedal point is the center of the nine point circle?
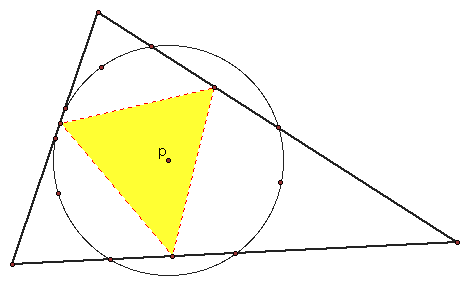
To change the shape of triangle ABC to see how the pedal point changes, click here.
We can see that the pedal triangle moves around inside triangle ABC, and it appears to be in another plane at some points as in the picture below.
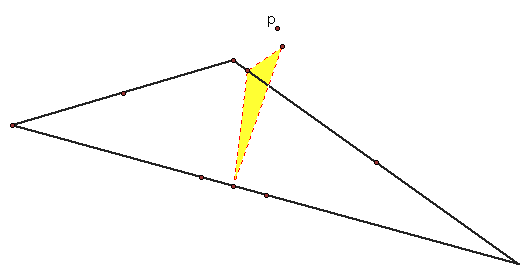
What if the pedal point (p) is on one of the sides of triangle ABC?
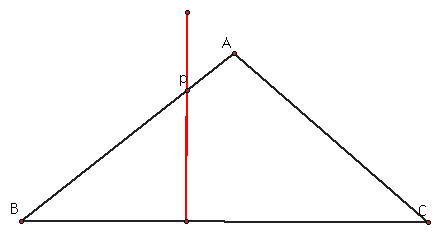
We can see that the pedal triangle is a segment. To change the shape of triangle ABC to see if a pedal triangle forms click here.
We can see that the points still form a segment not a triangle.
What if the pedal point is on one of the vertices of triangle ABC?
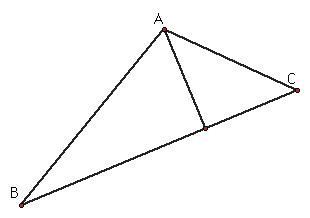
The pedal triangle forms a line that forms the perpendicular bisector of the opposite side.
Click here to move triangle ABC to see how the pedal "line" moves.
Find all conditions where the three vertices of the pedal triangle are collinear.

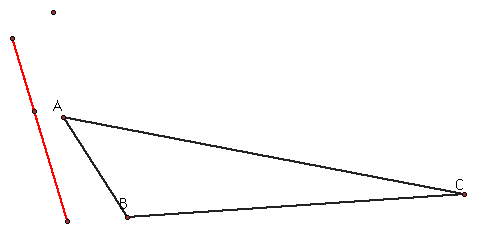
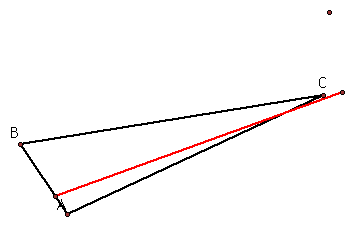
This line is called the Simson Line.
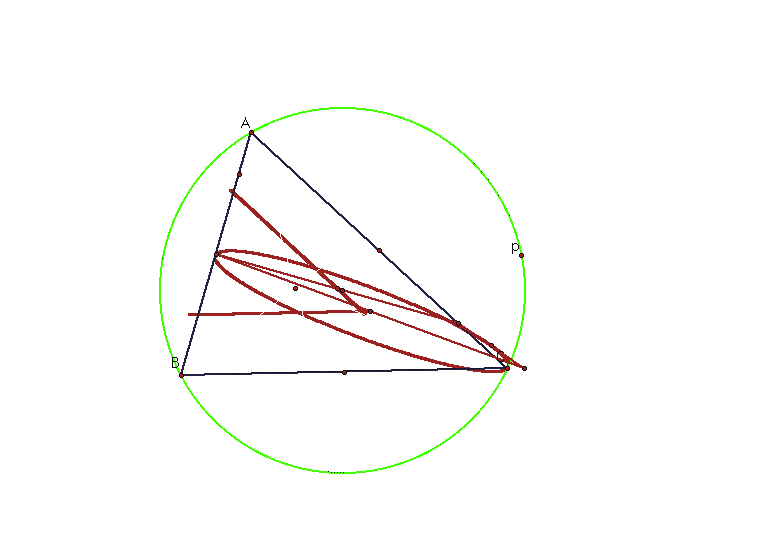
Locate the midpoints of the sides of the pedal triangle. Construct a circle with the center at the circumcenter of triangle ABC such that the radius is larger than the radius of the circumcircle.
Trace the locus of the midpoints of the sides of the pedal triangle as the pedal point p is animated around the circle you have constructed.
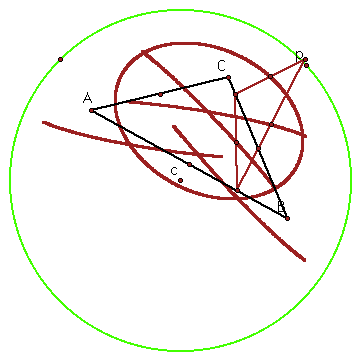
To see how the pedal point triangle changes, and to change triangle ABC to see how the traces change click here.
We can see that one path forms an ellipse. It appears that the other two paths are trying to form an ellipse but cannot complete their path.
What if the circle is the circumcircle?
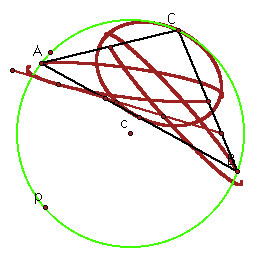
We can see that all three paths are forming an ellipse. Two of the paths have small breaks in their path. To animate the pedal point click here.
Construct lines on the sides of the pedal triangle. Trace the lines as the pedal point (p) is moved along different paths.
To see how the lines move click here.
Find the envelope of the Simsin Line as the pedal point is moved along the circumcircle.
To see the image as the pedal point is traced click here.
Repeat where the path is a circle with center at the circumcenter with a radius less than the radius of the circumcircle.
To see the image as the pedal point is moved around the circle click here.
Is there a point on the circumcircle for P (on the circumcircle) that has side AC as its Simson Line? What about AB? BC?
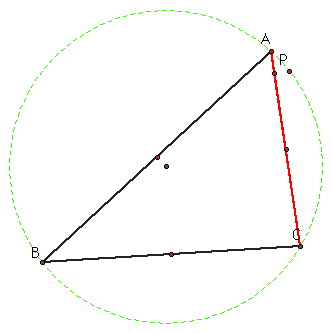
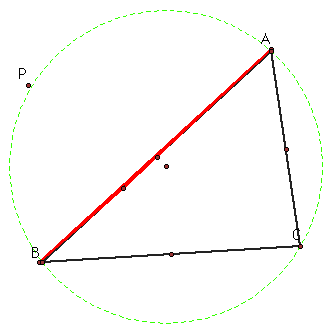
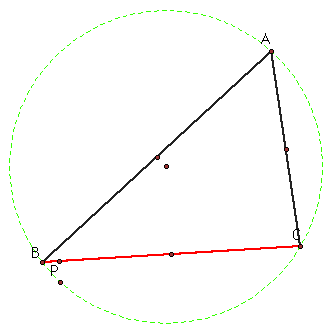
As we can see from these three pictures, there is a point for pedal point P on the circumcircle where AB, AC, and BC are the Simson line
Construct the Simson line of a point P (on the circumcircle) that connects P to the orthocenter. How do the two segments intersect?
The Simson line and the base of the triangle intersect at a right angle.
Select two pedal points on the circumcircle and compare the angle of intersection of the two Simson lines with the angular measure of the arc between the two pedal points.
To see how the angles change click here.
Animate the Pedal point (p) about the incircle of triangle ABC. Trace the loci of the midpoints of the pedal triangle.
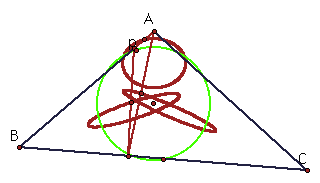
To animate the pedal point click here.
Repeat if triangle ABC is a right triangle.
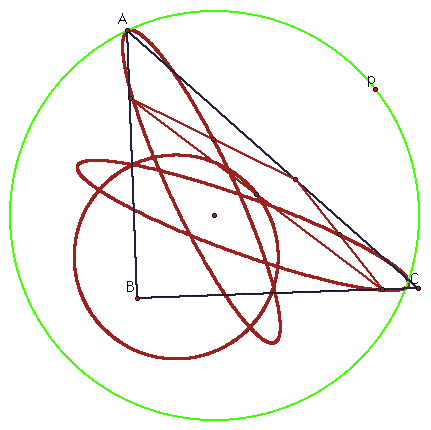
To animate the pedal point click here.
Construct an excircle of triangle ABC. Animate the pedal point about the excircle. Trace the loci of the midpoints of the sides of the pedal triangle. What curves result?
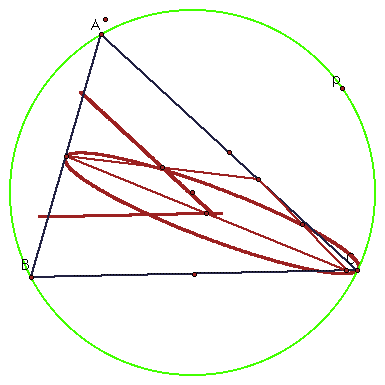
Two of the loci appear to form a triangle while the third locus forms an ellipse.
To animate the pedal point click here.
Look at the angle bisectors. How are the loci positioned?
The loci move around the angle bisectors.