Clay Bennett

Assignment 7.14

For this assignment, I choose to undergo the task of constructing a circle tangent to an abitarary point on a circle and a line out side of the circle. If there is a hell, I am going there because of this problem. I have cussed, fussed, and thrown a lot of things because of this problem. I probably should have given up on it a long time ago, but I kept telling myself that I’ve put too much time into is already so I stuck it out. Well, I’ve finally got it. I this problem just like any maze; from the end.

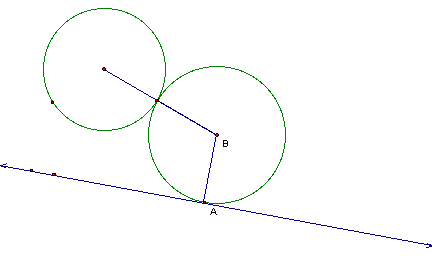
I realized that points of tangency with the line and circle would form a isosceles triangle with the center of my constructed circle. I also knew that the center of the my constructed circle would be collinear with the center of my given circle. From there I went to work.

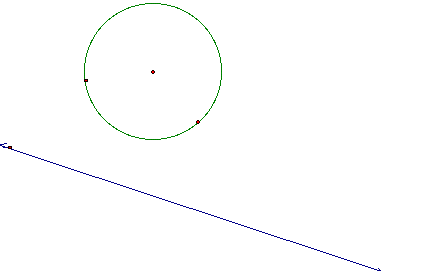
I began with my circle, point of tangency, and a line.

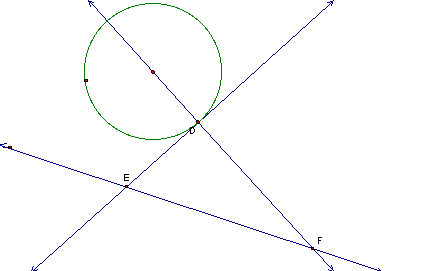
From here I constructed a line passing through the center and my point of tangency. I then constructed a line tangent my given tangency point. Next I marked where they intersected my line.

Now I take the angle bisector of angle DEF. The intersection of the bisector and line DF will give me the center of my constructed tangent circle.

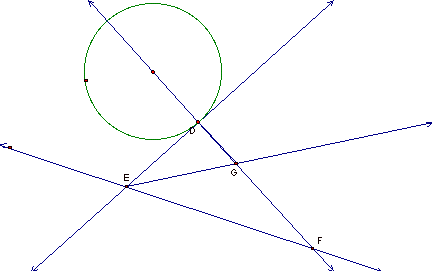
Finally, I construct a circle with a center of G and a radius of length DG and I have a circle tangent to my given circle and line.

If you would like to see the script for GSP then go to my assignment 5.