
Clay Bennett
Assignment 9
In this assignment I will be exploring the pedal triangle. Until this course, I had never heard of a pedal triangle, so everything in this investigation will be completely new to me. I will start with a picture of a pedal triangle.
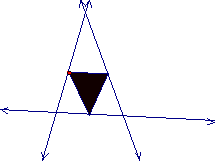
The
triangle with the yellow interior is the pedal triangle. The point on the outside of both
triangles is what is known as the pedal point. This point is what determines the size and position of the
pedal triangle. Here is a list of
steps on how to construct a pedal triangle…
Begin
with a given point, P any where on the plane. Then construct three lines, {a, b, c} such that a U b, b U
c, c U a (forming a triangle ABC).
Next, construct perpendicular lines passing through P with lines a, b,
and c. Now mark the lines point of
intersection with the newly constructed perpendicular line passing through
point P. These new points of
intersection, A’, B’, and C’ are the vertices of the pedal
triangle. The final step is to
connect these points with line segments and this will construct a pedal
triangle. I would recommend
cleaning up the construction by erasing or hiding, in the GSP case, the
perpendicular lines that were constructed.
Now
that I have completed the construction of the pedal triangle I will now
investigate its properties under certain given conditions. I will begin by looking at it when my
pedal point P is the incenter of triangle ABC. I will begin each case with a picture of the circumstance
given. Here is the picture of a
pedal point P as the incenter of triangle ABC.
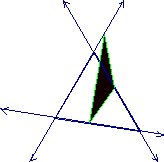
From
this picture you can see that when P in equal to the incenter of the triangle
that length of segments TC and SC are equal.
Next
is the case of when P is the Orthocenter of triangle ABC. Here is the picture…
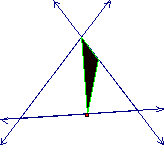
From
this picture, I can see that A is equal to R. This even holds true when the
orthocenter is outside of the interior of the triangles.

Now
I will examine the pedal triangle when the pedal point is the
circumcenter.
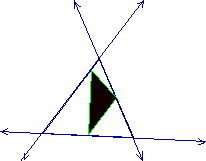
From
this picture we can see that the vertices S and T of the pedal triangle are the
midpoints of sides AC and BC of the triangle ABC. From the following picture we see that this holds true even
when the circumcenter is outside the interior of the triangles.
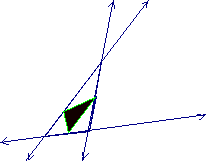
Next,
I will examine the pedal triangle when point P is the center of a nine-point
triangle…
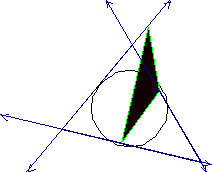
This
picture shows us that the vertice S is a midpoint of points 8 and 7 and vertice
T is a midpoint of points 4 and 5.
This
concludes my investigation of pedal triangles and the special case for point
P.