Clay Bennett

Final Assignment

Part A:

Here are some pictures of different triangles with the point p in different positions.

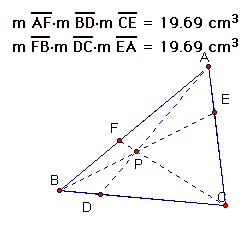
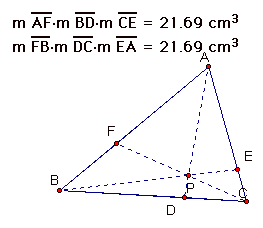
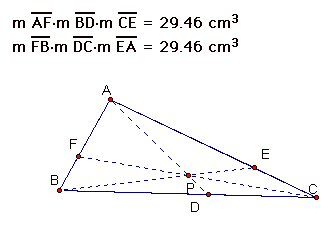
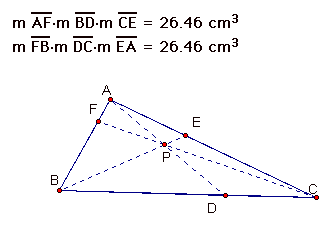
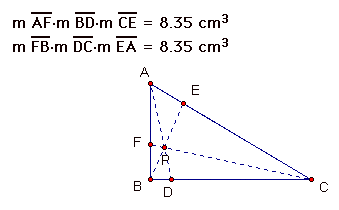
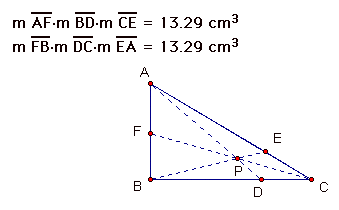
After examining the products of the segments I have conjectured that (AF)(BD)(CE) = (FB)(DC)(EA), which implies [(AF)(BD)(CE)]/[(FB)(DC)(EA)] = 1.

Part B:

Conjecturing is the easy part. Now I must prove this conjecture. In order to do this I must construct some similar triangles. This can be done by constructing lines through B and C that are parallel to AD and then extending the segments BC and CF to intersect with these new lines. It will look like this.

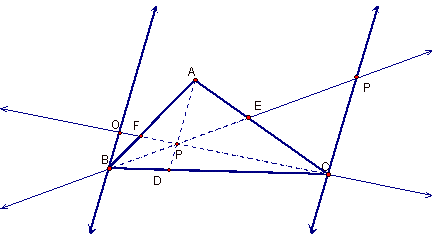
By using vertical angles and the alternate interior angle theorem I can deduce that triangle OFB is similar to triangle PFA and that triangle QEC is similar to PEA. Since I know the these triangle are similar, I can deduce that (i) (AF)/(BF) = (AP)/(BO) and that

(ii) (CE)/(AE) = (CQ)/(AP).

Now by using common angles (every angle is congruent to itself) and again, the alternate interior angle theorem I can find two more sets of similar triangles. These triangles are triangle BDP is similar to triangle BCQ and triangle BCO is similar to triangle DCP. The similarity of these triangles implies

(iii) (BD)/(BC) = (DP)/(CQ) and

(iv) (BC)/(DC) = (BO)/(DP).

Now by multiplying the equations, (i), (ii), (iii), and (iv), the following equation is formed.

[(AF)/(BF)][(CE)/(AE)][(BD)/(BC)][(BC)/(DC)] = [(AP)/(BO)][(CQ)/(AP)][(DP)/(CQ)][(BO)/(DP)]

After simplifying this equation I got

[(AF)(CE)(BD)]/[(BF)(AE)(DC)] = 1.

This is the result I needed to prove my conjecture.

Part C:

Here are some GSP pictures to show that the ratio of the two triangle areas is greater than four.

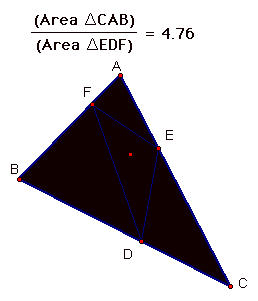
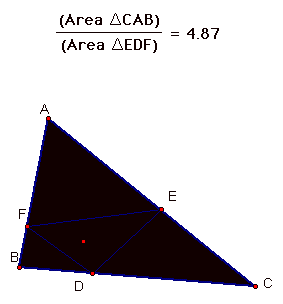
After playing around with the point P, I noticed that the ratio got larger when P was close to a side of triangle ABC. When P was near the center, it the ratio got closer to 4. Here is when the value is exactly 4.

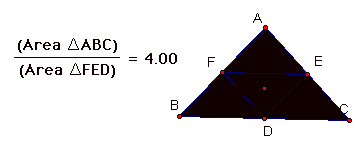
I must admit that it took me a while to figure out the significance of this P. After staring at it a while, I noticed that the vertices of the small triangle looked like the midpoints of the sides of the large triangle. I measured them to check and I was correct. This means that P must be the centriod in order for the ratio of the areas to be equal to 4.