Sinje J. Butler

Write-up 2

Let’s begin with the equation

where n= 4, 2, 0, -2, and -4.

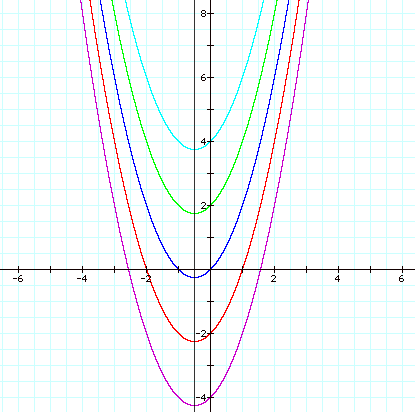
From this series of graphs it appears that each parabola has the same axis of symmetry and that as the value for n is changed, the vertex of each parabola moves up and down this axis of symmetry. It is also possible to show that the axis of symmetry for each of these graphs is -0.5 by recalling that the formula for the axis of symmetry is

where in

a = 1 and b = 1. Thus x = -0.5.

Let’s interpret the graph of

where a = 4, 2, 0,- 2, and - 4.

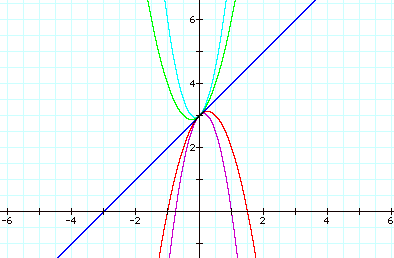
It appears that as the value for a decreases from a positive integer to a lower positive integer, the parabola begins to open up wider. Also notice that the axis of symmetry moves left. When the value for a is zero the parabola becomes a line. If a = 4 is changed to a = - 4 the parabola appears to rotate180 degrees. Note that all of the graphs have the common point of (0, 3). Is (0, 3) the only point that these graphs have in common? What is the significance of this point?

The following is the graph of

where b = 4, 2, 0,- 2, and – 4

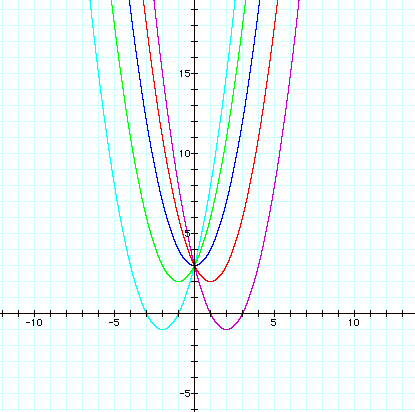
As the value for b = 4 changes, the vertex of each of these parabolas appear to move up the y-axis and to the right on the x-axis all the way through the graph where b = 0. Then the vertices move down the y-axis and to the right on the x-axis. These vertices appear to move in the shape of a parabola.

---

Return

---