Two Different Ways to Examine Roots Of

by

James W. Wilson and Sinje J. Butler

University of Georgia

It has now become a rather easy exercise, with available technology, to construct graphs to consider the equation

and to overlay several graphs of

for different values of b.

From these graphs discussion of the patterns for the roots of

can be followed.

For example, if we overlay the graphs of

for b = -3, -2, -1, 0, 1, 2, and 3, the following picture is obtained.

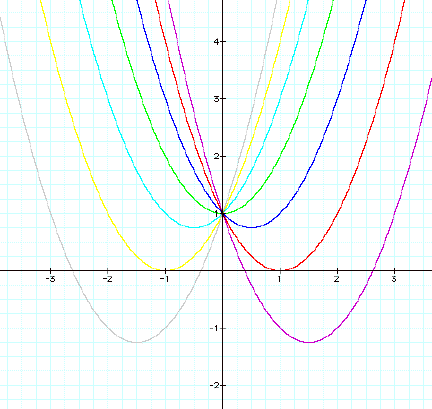
We can now discuss the movement of the roots of a parabola as b is changed. For

b < -2 the parabolas will each intersect the x-axis in two points with both having positive x values (i.e. the original equation will have two real roots, both positive). For b = -2 the parabola is tangent to the x-axis and so the equation has one real root at the point of tangency. That root is positive. For –2 < b < 2, the parabolas do not intersect the x-axis, therefore, the equations have no real roots. For b = 2, the parabola is tangent to the x-axis , thus, having one real, negative root. Finally, for b > 2, the parabolas will each intersect the x-axis twice to show each as having two negative real roots.

Graphs in the xb plane

Consider the equation

,

keeping in mind that we want to determine the roots of this equation for a given b.

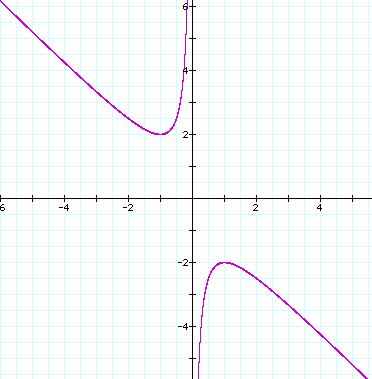
If we take any particular value of b, say b = 3, and overlay this equation on the graph we add a line parallel to the x-axis. If it intersects the curve in the xb plane, the intersection points correspond to the roots of the equation for that value of b. We have the following graph.

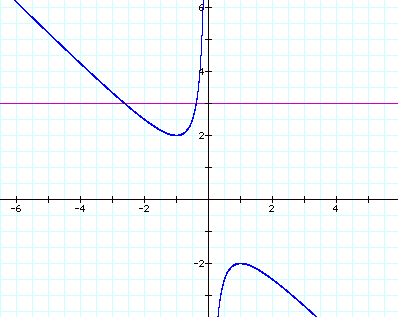
For each value of b we select, we get a horizontal line. It is clear on a single graph that we get two negative real roots for each equation when b > 2, one negative real root when b = 2, no real roots for the equations when –2 < b < 2, one positive real root when b = -2. Notice that this is the same conclusion we obtained by graphing

for b = -3, -2, -1, 0, 1, 2, and 3 and analyzing the individual graph for each value of b.

Plotting

gives a graph in the xb plane. This single graph, is the locus of the roots of

as b changes. Therefore, this is a graph of the movement of these roots as b changes.

This is one example of how the technology available today gives students the opportunity to easily explore different approaches to solving the same problem. The insight gained by exploring problems in this manner and the insight gained by taking the time to understand why these different approaches work yields a better understanding of the content being explored.

---

Return

---