Sinje J. Butler
Write-up 7
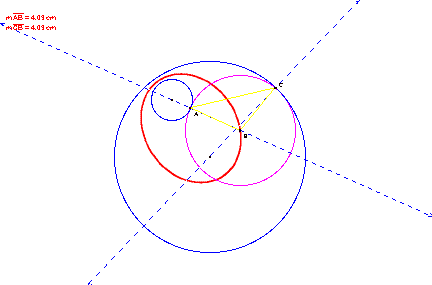
Please see attached graph for a script tool for the problem:
Given two circles and a point on one of the circles. Construct a circle tangent to the two circles with one point of tangency being the designated point.
Notice, that as the given point moves, the center of the constructed tangent circle moves in the path of an ellipse.
Above, we constructed a circle tangent to the two circles
with one point of tangency being the designated point. The smaller circle is external to the
tangent circle. From this point we
can also construct a tangent to the point where the smaller circle is internal
to the tangent circle. Please see construction, script tool and animation.
Notice, that as the given point moves, the center of the constructed tangent circle moves in the path of an ellipse.
One observation from this investigation is if you want to construct a tangent circle to two given circles when the given point is on the smaller of the two circles and the smaller circle is external to the tangent circle
you do the following.
Given the two circles and a point on the smaller circle, use the script tool above to generate the path of the center of tangent circles that are external to the smaller circle. Construct a line from the center of the small circle to the given point and construct a point of intersection where this line meets the path of the ellipse. Call this point B. B is the center of the desired tangent circle. Thus, line segment AB in the picture below is the radius of the tangent circle. Also, notice that when a line segment is generated from B to a point on the circle that is equal in length to segment AB, call this segment CB, you have the point of tangency on the large given circle.