
Sinje J. Butler
Write-up 8
The following is a sketch of triangle ABC with its orthocenter H.
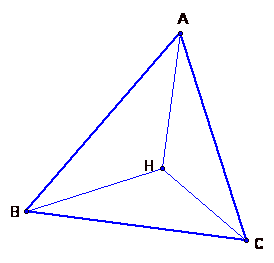
Take a look at triangles HBC, HAB, and HAC. What will the location of their orthocenters be?
Recall that the definition of the orthocenter of a triangle is the common intersection of the three lines containing the altitudes and use this definition to think through the process of determining the orthocenter for triangle HAC.
The altitude from vertex C
to line segment AH is a1
on the graph below. We
know this because the line containing segment AH
contains one of the altitudes of
the original triangle ABC, thus, this
line is perpendicular to line segment BC, further, the segment from the vertex C to the foot of the perpendicular on BC is perpendicular to the line
containing segment AH. The
line containing this altitude runs through line segment BC.
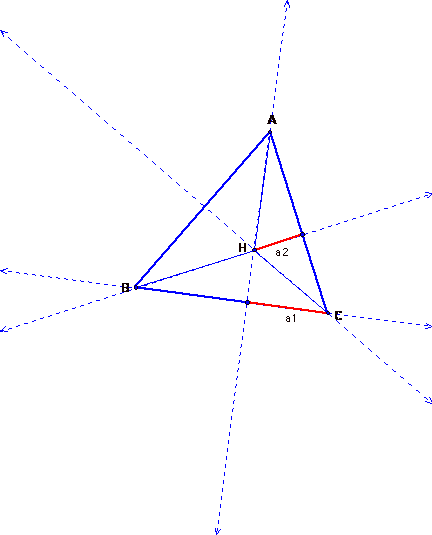
The altitude from vertex H to segment AC is a2 because the line containing a2 contains one of the altitudes of the original triangle.
It is now clear that the lines containing a1 and a2 intersect at vertex B of the original triangle. Since the orthocenter of a triangle can be determined by the common intersection of two lines containing the altitudes, the orthocenter of triangle HAC is vertex B of the original triangle.
By using this same line of reasoning you can state that the
orthocenter for triangle HBC is vertex A
and the orthocenter for HAB
is vertex C.
Please click here for a GSP demonstration. Notice for triangle HAC with orthocenter at vertex B, that when the orthocenter is outside the triangle, HAC appears to be an obtuse triangle. B appears to lie on top of vertex H when the triangle is a right triangle. And, finally when B moves into the triangle, the triangle appears to be acute. This is how we would expect the orthocenter to behave.