
Sinje J. Butler
Final Assignment
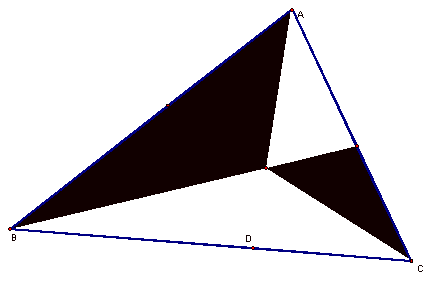
The following triangle has been constructed by considering any triangle ABC and selecting a point P inside the triangle. Lines AP, BP, and CP were drawn and extended to their intersections with the opposite sides in point D, E and F respectively.
Please click here for a GSP Demonstration exploring (AF)(BD)(CE) and (FB)(DC)(EA) for various triangles and various locations of P.
The GSP Demonstration suggests that for all triangles and all points of P, (AF)(BD)(CE) = (FB)(DC)(EA). Is this true? Even though it appears to be the case, the GSP Demonstration does not prove it to be true. Below is a proof of 1 case where this is true. The other cases are left for other explorations.
Let’s begin by proving
(AF)(BD)(CE) = (FB)(DC)(EA)
for the case of triangle ABC at point P that is pictured above. We will prove by constructing some parallel lines that produce similar triangles and using the related ratios. In coming up with a proof, the similar triangles that I constructed did not provide any segments that allowed for substitutions. Therefore, I used, www.cut-the-knot.org/Generalization/ceva.shtml for a hint on how to construct the correct similar triangles.
In the picture below, a line through point A parallel to segment BC was constructed. Segments CP and BP were extended to lines and there intersections with the parallel line through point A were marked as G and H respectively. Within this construction lie similar triangles that will be used for the proof.
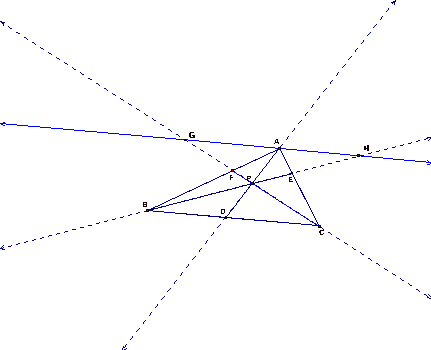
Angle GPA is equal to angle DPC by vertical angles. Also, because angle AGP and angle PCD are alternate interior angles, they are equal. So, by the AA Similarity Postulate
triangle GPA is similar to triangle DPC. Therefore, we know the following
![]() .
.

Also, from the above picture we can use the same line of arguing to show that triangle AHP is similar to triangle PBD. Angle HPA is equal to angle BPD by vertical angles. Also, because angle AHP and angle PBD are alternate interior angles, they are equal. So, by the AA Similarity Postulate triangle AHP is similar to triangle BPD. Therefore, we know the following
![]()
The ratio of the corresponding sides of triangle GPA and triangle DPC is equal to
the ratio of the corresponding sides of triangle AHP and triangle BPD. From this we can write the following
![]() .
.
Because
![]()
are line segments that we are not interested in, we can eliminate them and write the following for future use.
![]()
From the picture below, we can argue that triangle AHE is similar to triangle BEC.

Angle AEH is equal to angle BEC by vertical angles. Also, because angle AHE and angle EBC are alternate interior angles, they are equal. So, by the AA Similarity Postulate
triangle AHE is similar to triangle BEC. Therefore, we know the following
![]()
Because
![]()
contains segments that we are not interested in, we can eliminate it and write the following for future use.
![]() .
.
Triangle GAF is similar to triangle FBC.

Angle GFA is equal to angle BFC by vertical angles. Also, because angle AGF and angle FCB are alternate interior angles, they are equal. So, by the AA Similarity Postulate
triangle GAF is similar to triangle BFC. Therefore, we know the following
![]() .
.
Because
![]()
contains segments that we are not interested in, we can write the following for future use.
![]()
Recall the three sets of ratios that we established for future use.
(1) ![]() ,
,
(2) ![]() ,
,
and
(3) ![]() .
.
Number three can be rewritten as
![]() .
.
Number two can be rewritten as
![]() .
.
Plugging in number two and three into number one gives the following.
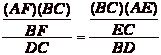
Which can also be written as
![]()
or
![]() .
.
Divide both sides by BC, which gives
![]()
or
![]()
Click here for a GSP Demonstration that suggests when P is inside triangle ABC, the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to 4. And it also appears that the ratio is equal to four when triangle DEF is the medial triangle. This is not a proof, it can be used for further exploration.