Note: This write-up is best viewed with a screen resolution of 1280 X 1024 (or higher). If viewing this page in a smaller resolution, please note that for the pairs of graphs below, when the text refers to the "left" graph, that is the "top" graph of the two graphs paired together that display one above the other in your browser. Likewise, the "right" graph and the "bottom" graph are the same.

For this exploration, we shall set out to compare the following polar equations:

where theta ranges from 0 to 2Pi. Additionally, we will hold a and b constant and a = b while varying k. For our first set of comparisons, we will set a = b = 1. Notice that there is no a in our second equation, so a = 0. We start with k = 0.

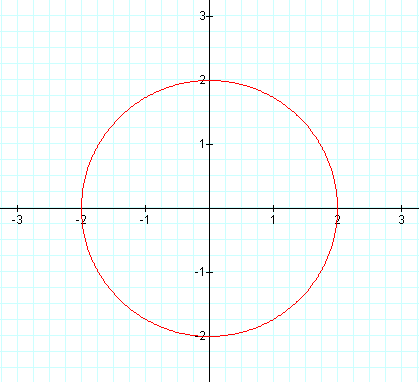
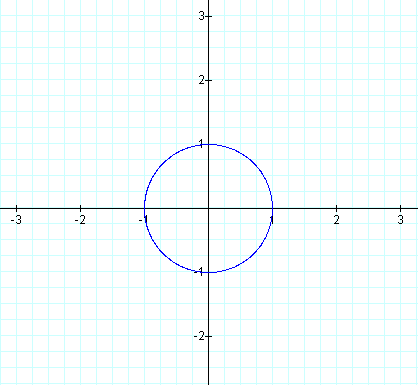
Under these conditions, we see that our graphs are similar. The graph on the left is a circle centered at the origin with a radius of 2, while the graph on right is a unit circle centered at the origin.
Now let's set k = 1. We obtain the following graphs:

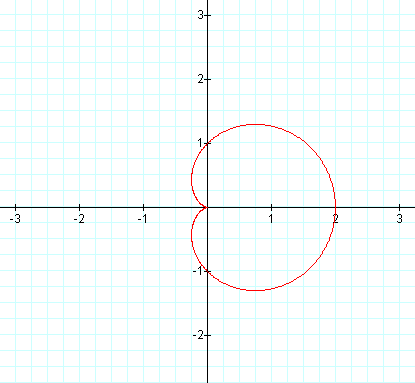
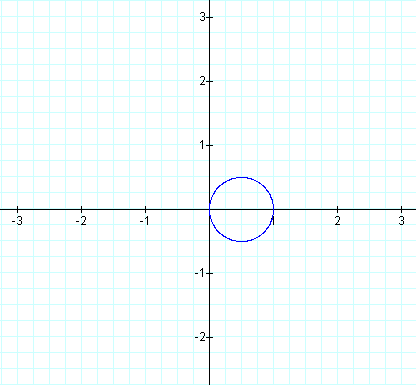
Here our graphs do not appear very similar. The graph on the left is called a "cardioid." On the right, we have what appears to be a circle centered at (1/2, 0) with a radius of 1/2. As with our first pair of graphs, we notice that the graph where a = 0 is "smaller" than the other one.
Next we set k = 2.

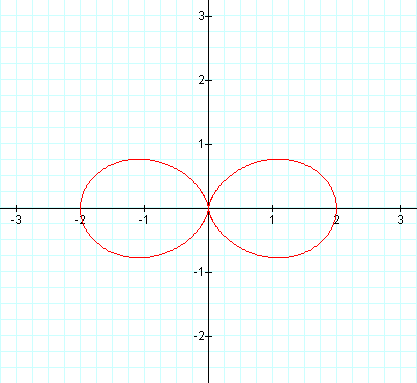
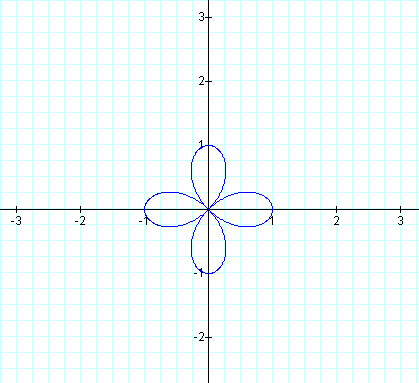
Our equation for the graph on the left is known as the equation of the "n-leaf rose" (we use k for Graphing Calculator since n is reserved) when a = b. And as should be expected we obtain a graph with 2 leaves. On the right our graph resembles a smaller version of the 4-leaf rose.

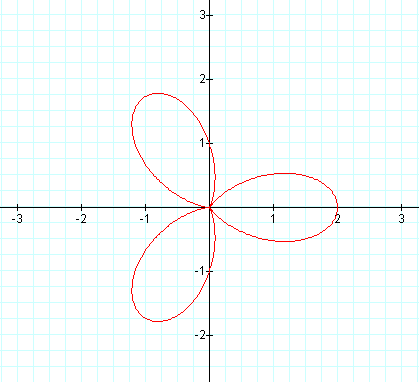
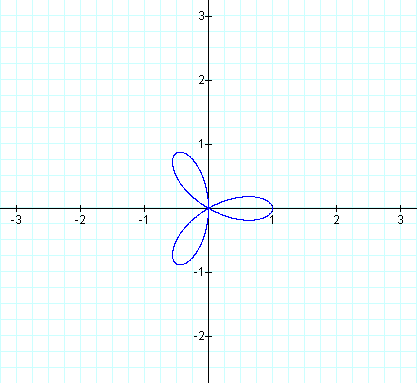
As expected, our graph on the left is a 3-leaf rose. Our graph on the right is not a 6-leaf rose, but rather it is also a 3-leaf rose, just smaller. What do you expect the next pair of graphs to be?

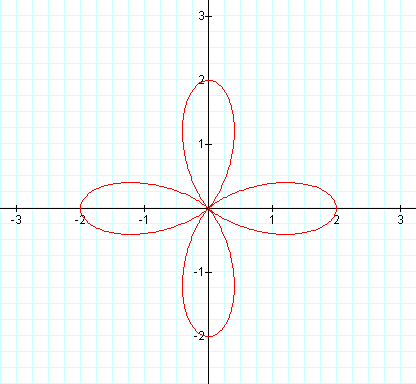
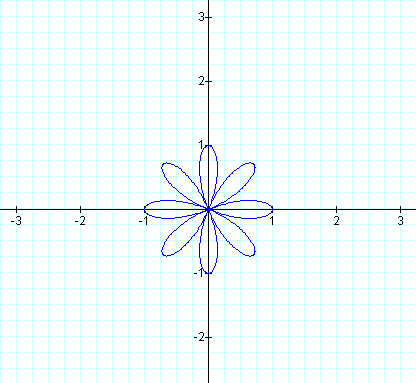
Just as we would expect the graph on the left is of a 4-leaf rose, but what about the graph on the right? Once again, we have a rose with twice the number of leaves as our first graph, which gives us an 8-leaf rose.
Now we set a = b = 2 (except where a = 0), and vary k. What graphs do we get?

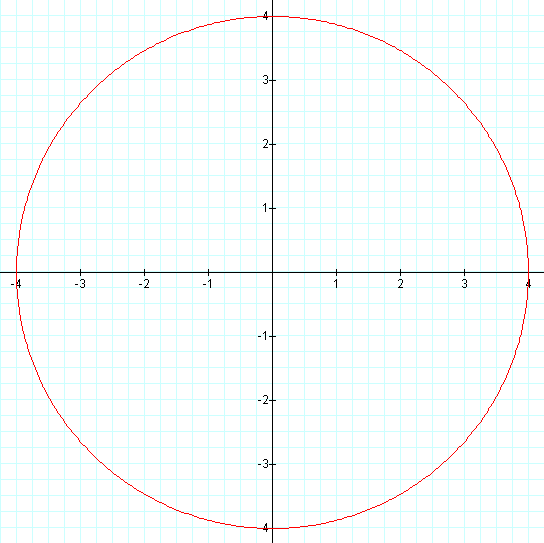
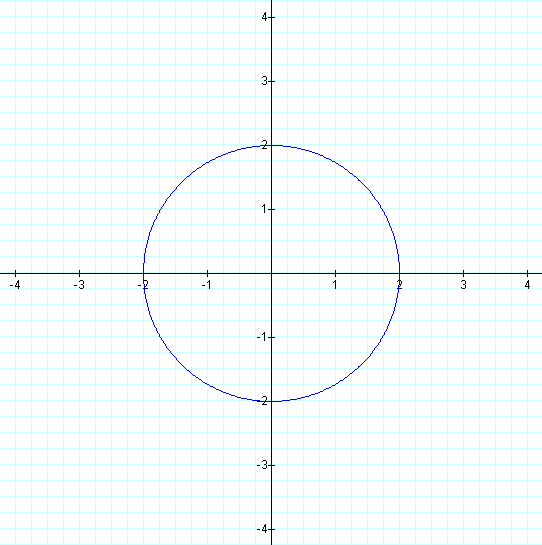
Two circles whose radii are twice what they were previously...

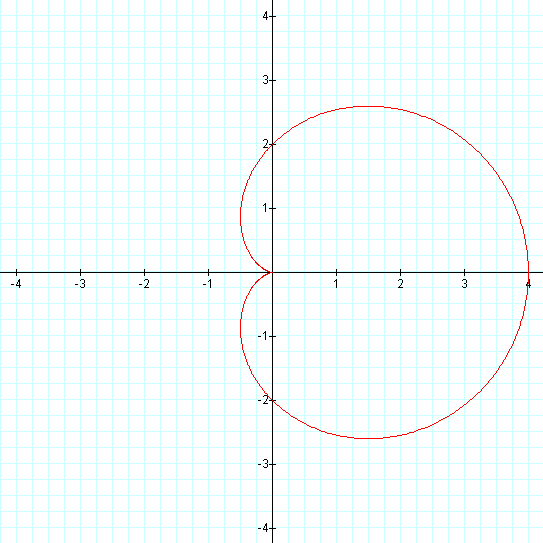
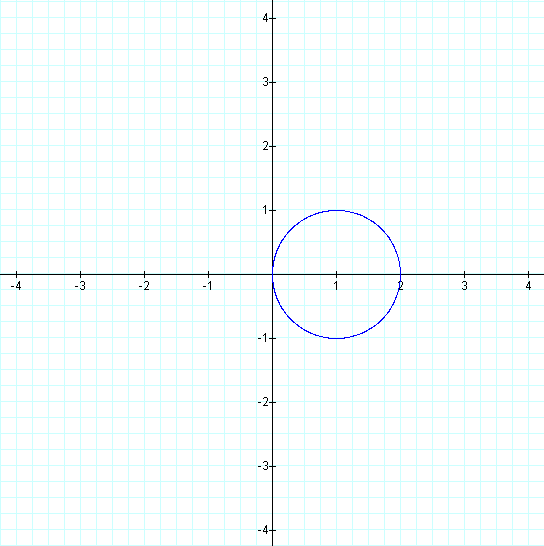
Graphs twice the size of our previous ones for k = 1...

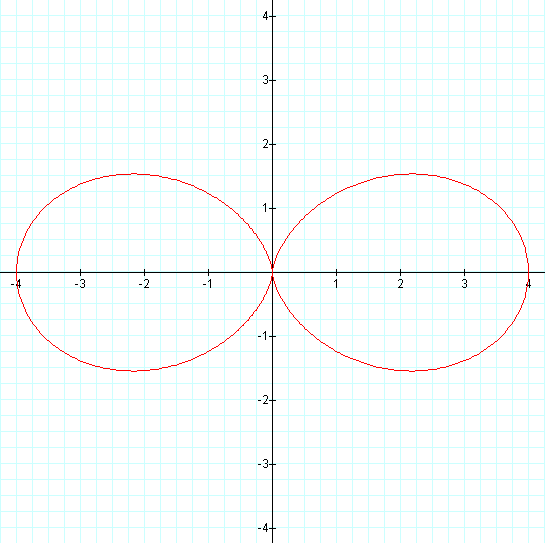
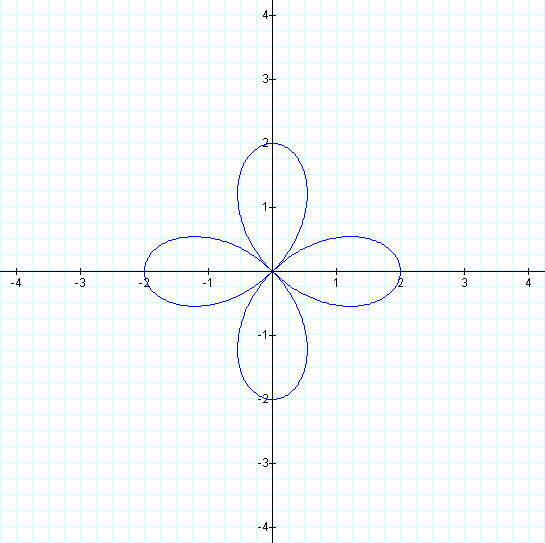
A 2-leaf rose and a 4-leaf rose twice the size as before...

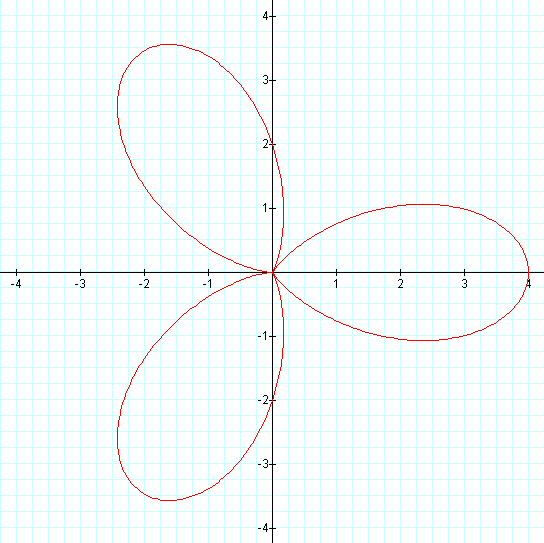
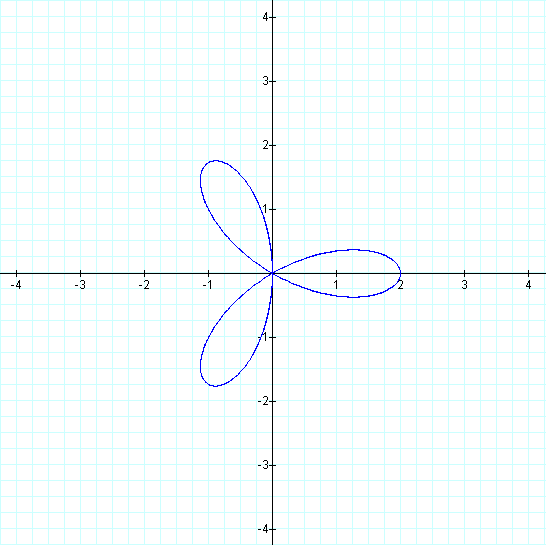
Two 3-leaf roses... and... can you guess what is next?

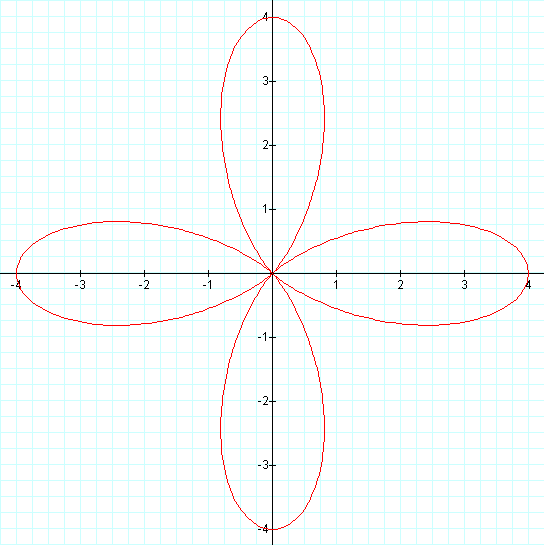
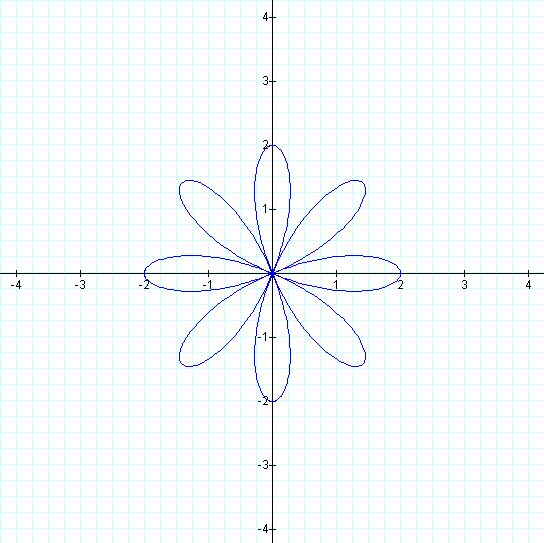
A 4-leaf rose and an 8-leaf rose twice the size of the previous ones, just as you expected, right?
The following two graphs are overlays of the graphs when k = 4, and we let a and b vary from 1 to 3.

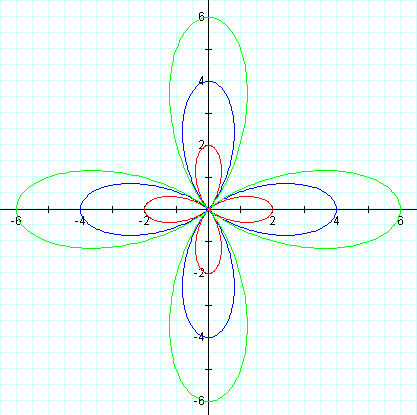
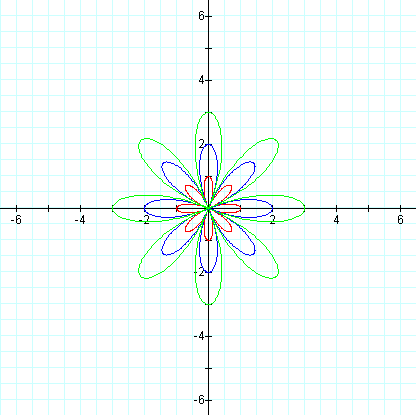
As further investigation, let's take the first of our equations and replace cosine with sine so that we have:

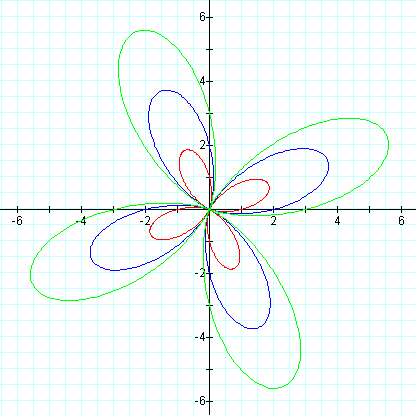
Observe the following graphs where a = b = 1, and k varies from 0 to 4. Followed by a composite graph of a = b varying from 1 to 3 with k = 4. What do you notice about these graphs?

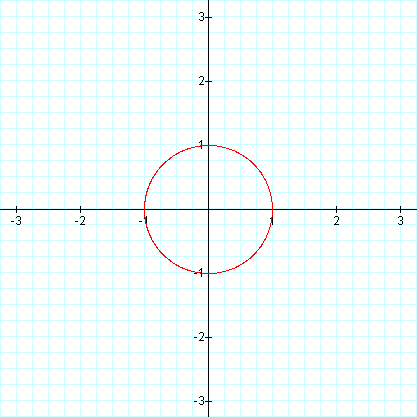
We can see that this graph mimics the cosine graph when a = 0, b = 1, and k = 0. What about the following graph?

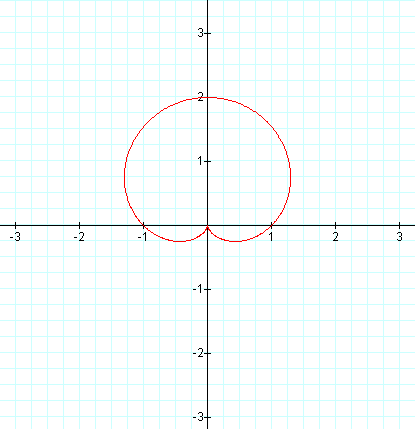
This graph is similar to the cosine graph for a = b = k = 1. The graph appears to have been rotated 90 degrees counter-clockwise about the origin. Examine the next graph.

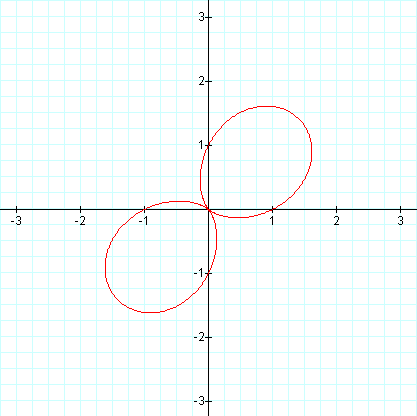
As with the cosine graph with the same coefficients, we get two leaves. Here the leaves appear to have been rotated counter-clockwise by 45 degrees about the origin. Does the next graph result in three leaves?

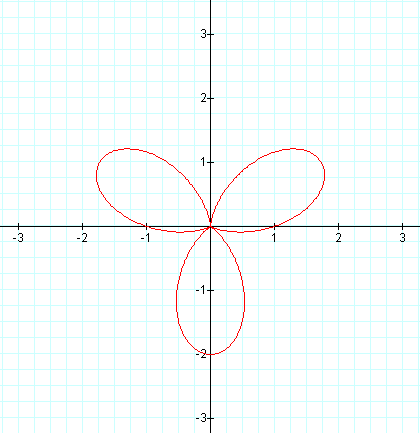
As expected we get three leaves in this graph. This time our rotation appears to be 90 degrees clockwise about the origin.
Will our last graph be a rotation of the cosine graph about the origin?

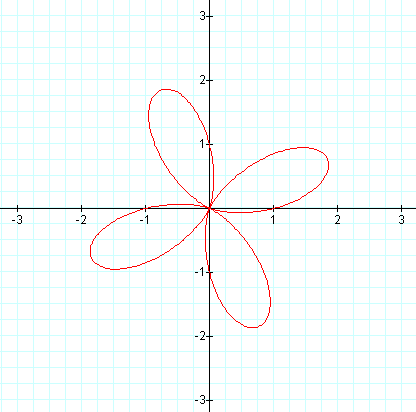
The answer to our question is yes. This graph appears to be the same as the cosine graph only rotated 45 degrees counter-clockwise about the origin.