Let us began by stating the problem we wish to solve.
Statement of Problem:

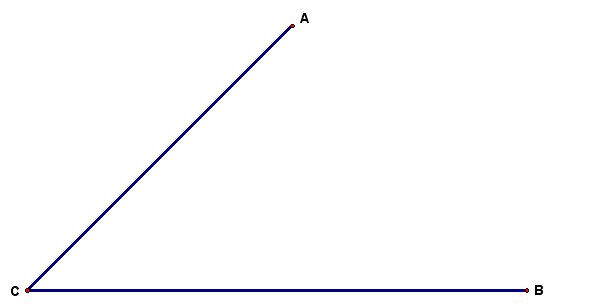
Our first step is to construct the segment AB, essentially completing the triangle. Here, we draw it with a dotted line as it is only used for construction purposes. Also, we identitify an arbitrary point, say X', on the segment AC.

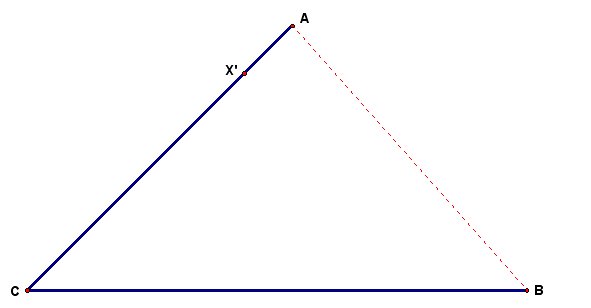
Next we construct a circle about point X' with a radius the length of segment X'A. Then we can construct a line parallel to segment CB passing through X'. We now mark the point in the interior of Angle ACB which is the intersection of our circle about X' and the parallel line passing through X'. Here we call it point n.

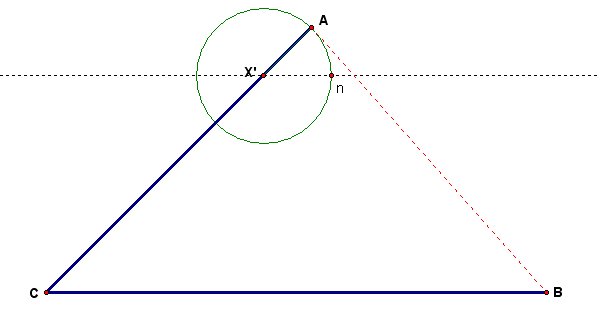
Next we wish to find a point, say z, on segment AB such that X'n = nz. To do this we construct a circle about point n with radius equal to the length of X'n. Then we construct the intersection of the circle and segment AB. In the following illustration, our circle about X' has been hidden.

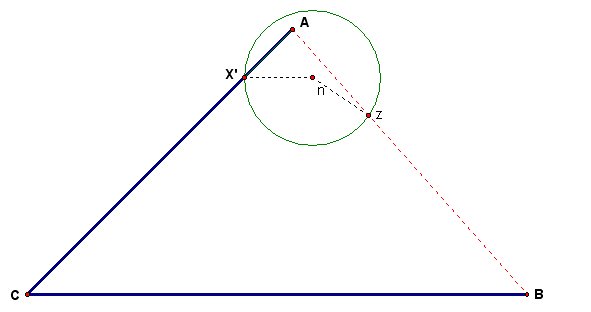
We now have three points X', n, and z and two segments X'n and nz which are equal in length. Thus, we can construct a rhombus by finding the fourth point, say Y', such that X'n = nz = zY' = Y'X'. To do this, we can hide our circle about point n and redraw (or "unhide") our circle about point X'. Then we construct the line passing through point X' that is parallel to nz. The intersection of this parallel line and our circle about point X' which is in the interior of Angle ACB is our point Y'. We now have our rhombus.

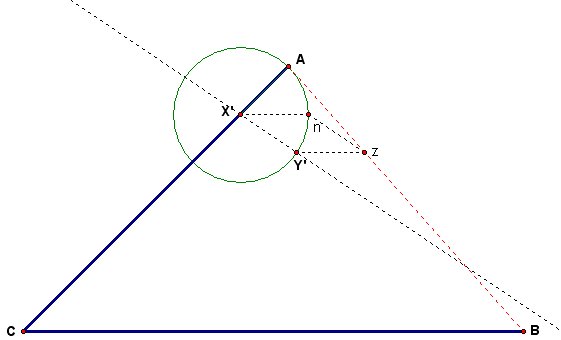
Using our rhombus, we can determine the location of point Y. First we construct the ray AY'. The intersection of ray AY' and segment CB is point Y. This is the projection of Y' onto segment CB.

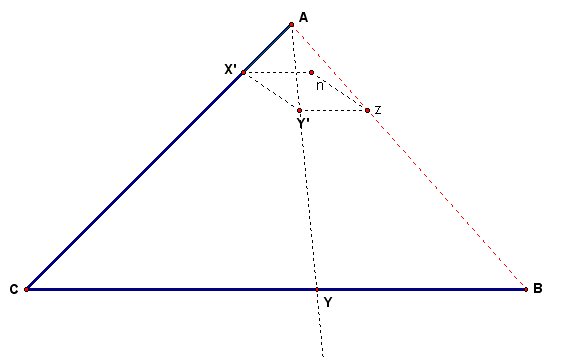
We now have the segment YB that we need. We must construct point X. To find X, we construct a circle about point A with a radius equal to the length of segment YB. The point at which the circle intersects segment AC is point X.

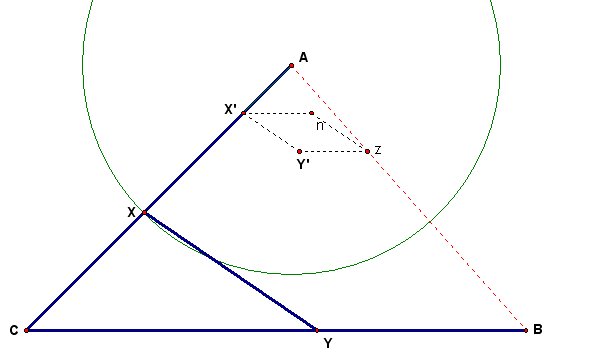
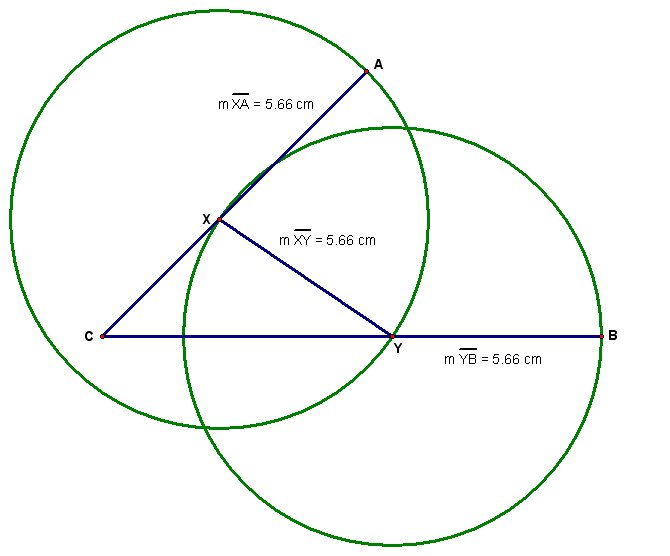
Finally we have points A, B, X, and Y such that AX = XY = YB. The following illustration shows circles about points X and Y with radius equal to the length of XY. For those who must have "numbers" rather than faith in the construction, the illustration allows contains the lengths of AX, XY, and YB.