

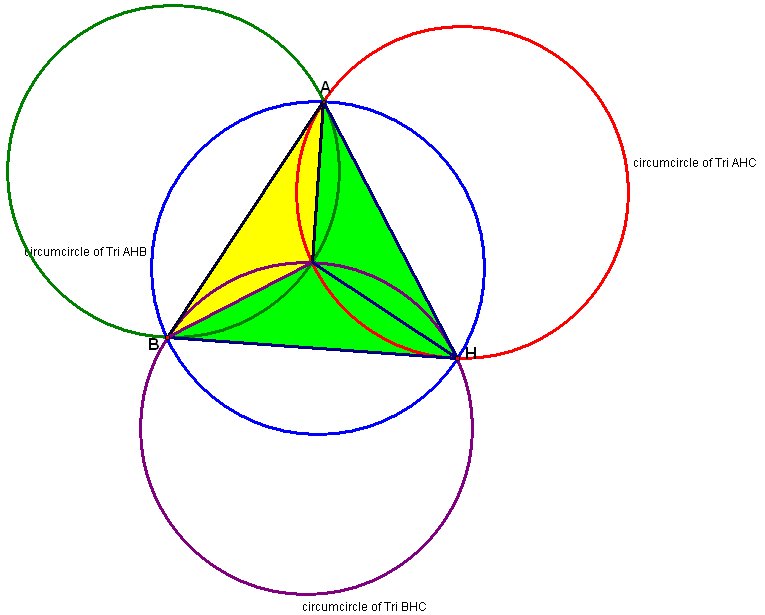
Using either the tools from previous explorations, or just the knowledge gained from them, we can construct a Triangle ABC and its orthocenter H. Additionally we can construct the circumcircle for Triangle ABC. Using H, we can construct the Triangle AHB, Triangle BHC, and Triangle AHC. Again we can construct the orthocenters. We find that the orthocenter of Triangle AHB is C, the orthocenter of Triangle BHC is A, and the orthocenter of Triangle AHC is B. We can also construct the circumcircles of these additional triangles. Your result should be similiar to the following illustration.
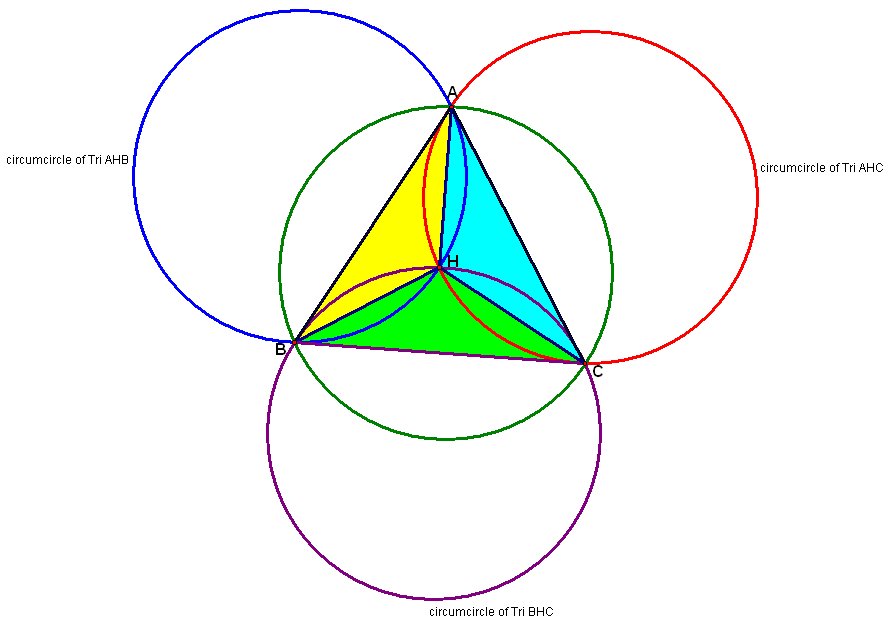
We construct the alititudes of Triangle ABC by constructing perpindiculars from each vertex to the opposite side. Notice that each passes through H. If we also construct the intersection of each altitude with the circumcircle and then construct the segments from those points to H and to the two vertices not along that point's altitudinal line we see a familiar figure. Here those lines are dashed, and we see the outline of a cube.
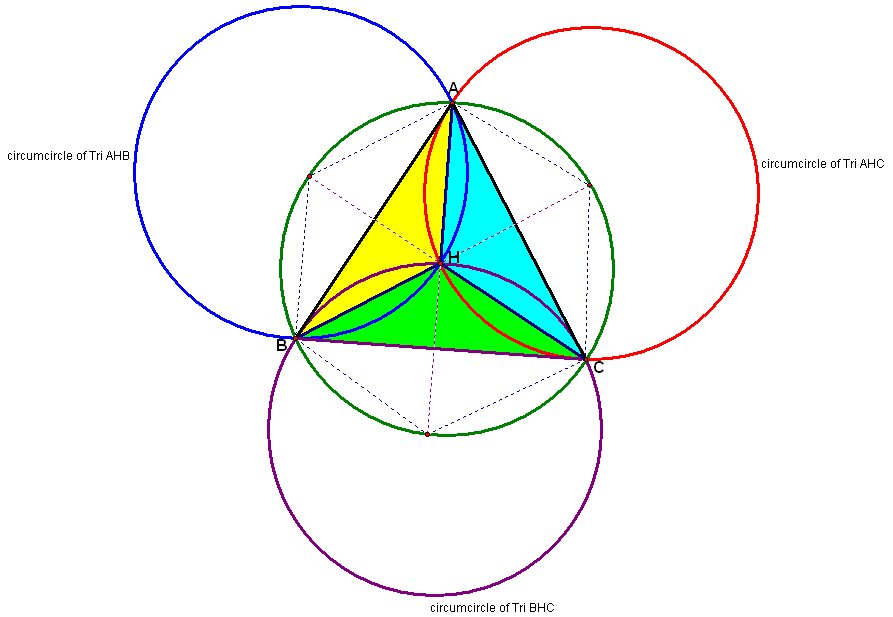
What would we observe if we moved point A to where H is located? Where would H then be located? How would our figure change? Consider the following illustration.
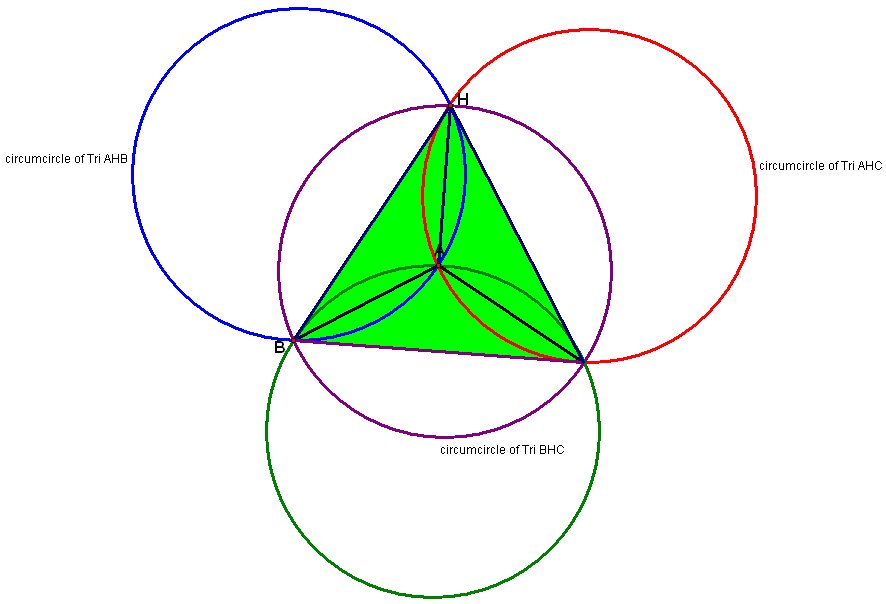
We see that when A is located where H was originally, that H then becomes located where A was. In addition, while the parts of our figure have different meanings, we see that we obtain the same figure! Is A itself special? Let's trying moving point B to where H was in the original. The following is our result. What do you observe?
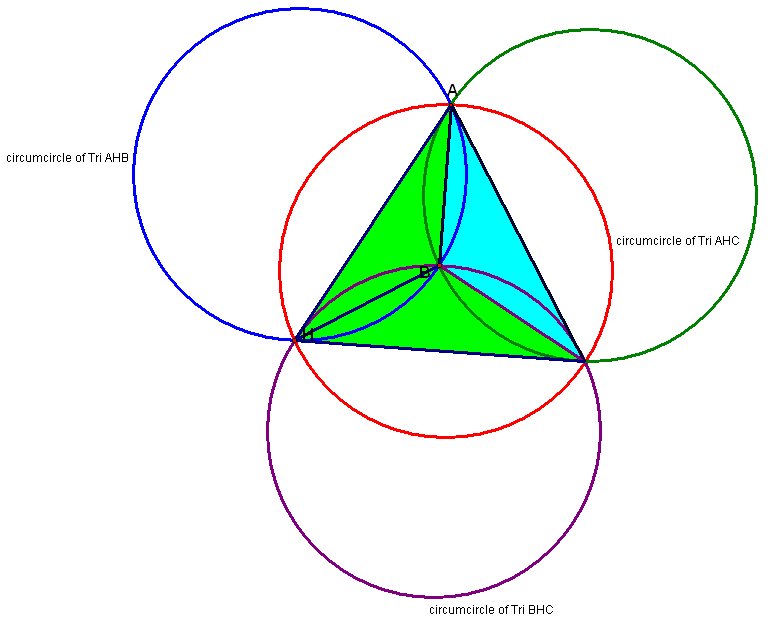
Again we obtained the same figure. Do you doubt that we will get the same result if we move C to the original location of H? Here's the ilustration.
Cool, don't you think? Click here for a GSP file where you can animate this process for yourself and see what is happening as each vertex moves.
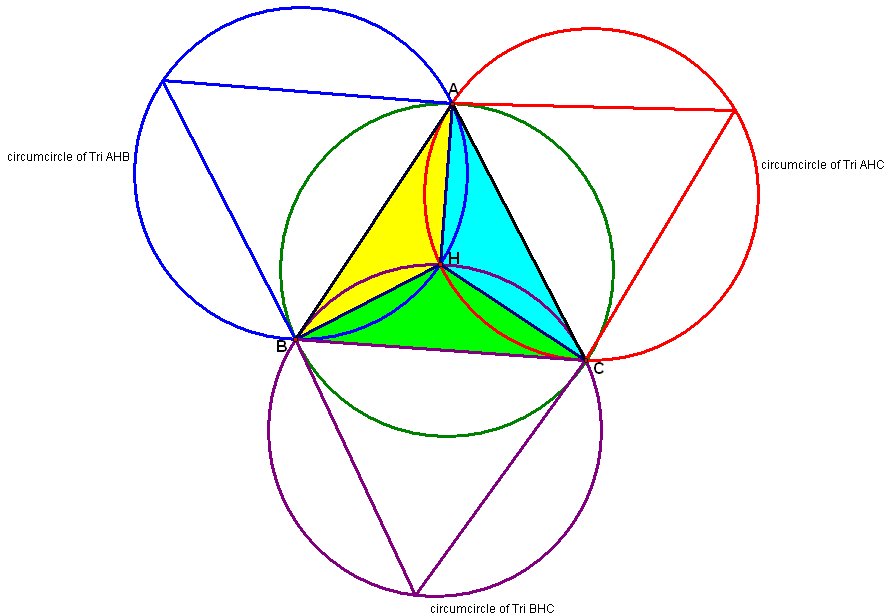
We close with an interesting illustration. Choose a side of the original triangle, say segment AB. Use this as your "mirror" and reflect Triangle ABC across it. What do you notice? Repeat the process for segments BC and AC. Did you obtain something similiar to what follows? Can you relate this to other explorations?
| Return to main page. |