EMAT 6680 Write-Up for Final Assignment by Robert Childres

An Exploration with a Triangle and a Point

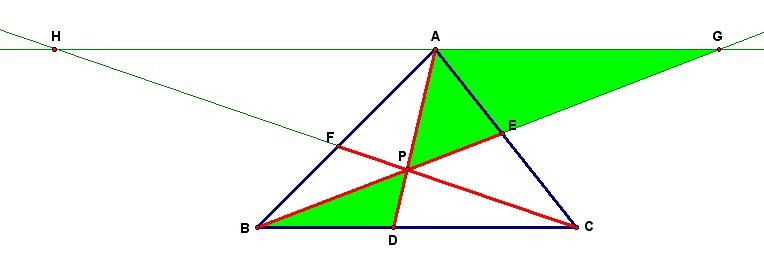
Let's consider any Triangle ABC. We then select any point P in the interior of our Triangle ABC and construct the lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively. The following illustration is one such situation.

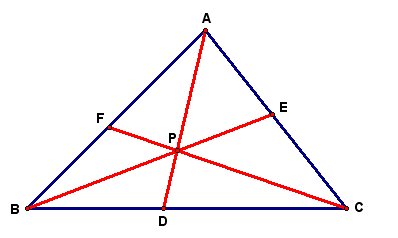
Click here for GSP tool to create a triangle and and these segments when P is inside the trianble. Use this tool to explore different configurations of Triangle ABC. Now explore (AF)(BD)(EC) and (FB)(DC)(EA) for different triangles and various locations of P.

Now we wish to consider the following relationship:

In order to examine this relationship, we will need to construct some similar triangles. We start by constructing a line through point A that is parallel to (BC). In addition, we extend (BE) and (CF) in order to construct the intersection points G and H respectively. We now have the following configuration.

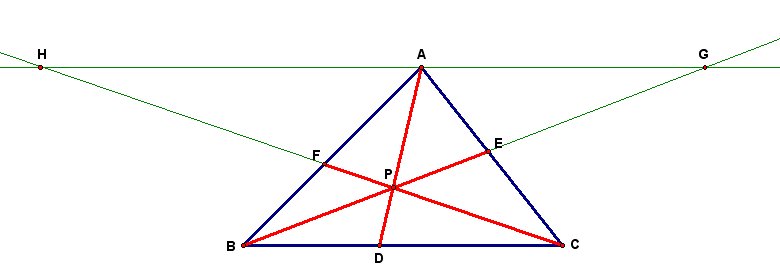
Let us first look at the similar triangles AFH and BFC as shown in the next illustration.

Since corresponding sides of similar triangles are proportional, we obtain the following relationship:

Now let's examine the triangles AEG and BEC as shown below.

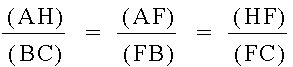
We now obtain this relationship:

Now let's examine the triangles APG and BPD as shown below.

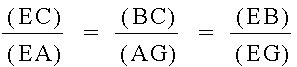
The relationship we find in these similar triangles is:

Now let's examine the triangles APH and CPD as shown below.

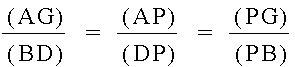
From here we have:

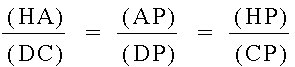
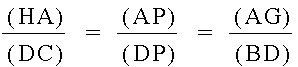
Using the last two relationships, we see that: (HA)/(DC) = (AP)/(DP) = (AG)/(BD)

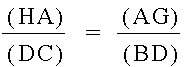
Doing some algebra we have the following: (HA)/(DC) = (AG)/(BD)

We now have all we need to demonstrate the relationship of our orginal segments. From the above work we have the following relationship: [(AF)(BD)(CE)]/[(BF)(CD)(AE)] = [(AH)(BC)(AG)]/[(BC)(AG)(HA)]

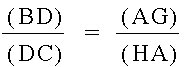
[(AF)(BD)(CE)]/[(BF)(CD)(AE)] = [(AH)(BC)(AG)]/[(BC)(AG)(HA)]

It should be plainly obvious that the right-hand side simplifies quite nicely to one. Therefore, we have proven that the following relationship holds: [(AF)(BD)(CE)]/[(BF)(CD)(AE)] = 1

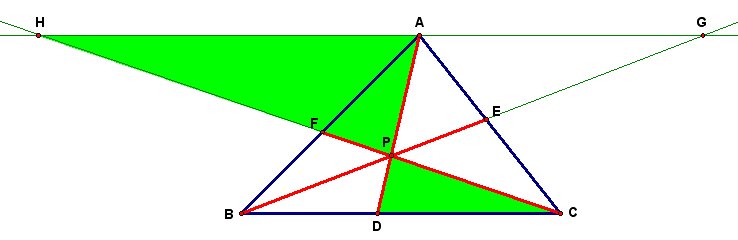
We can also extend this to when P is outside of Triangle ABC. The following is one such illustration. Also included is a GSP tool for when point P is outside of the triangle.

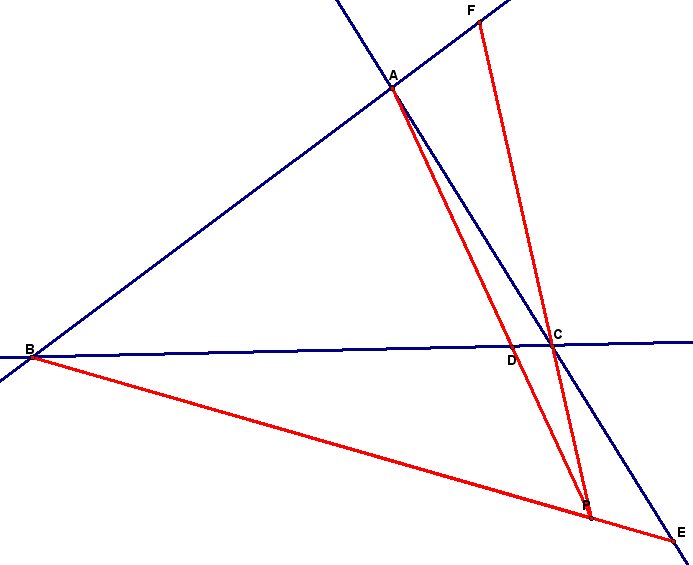
Click here for GSP tool to create a triangle and and these segments when P is outside the triangle.

Interestingly, the ratio of the area of Triangle ABC to the area of Triangle DEF is always greater than or equal to 4. Can you come up with the proof on your own? The following illustration shows a configuration where the ratio is equal to 4. Do you recognize the location of point P? Point P is located at the centroid of Triangle ABC. Included below is a GSP file where you can play with the location of point P and see how that affects the ratio of the areas.

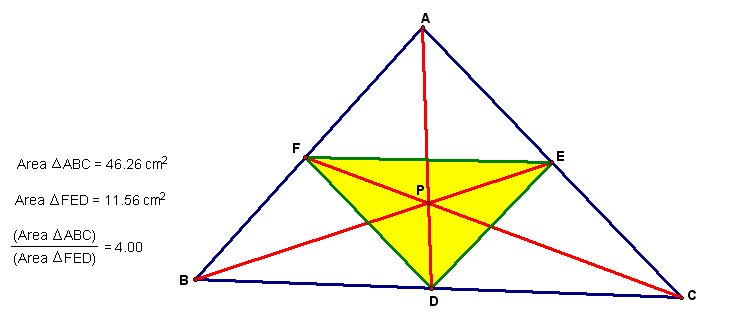
Click here for GSP file to explore this relationship..

Return to main page.

Write-up by Robert Childres.