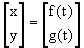Assignment 10: Parametric Curves

by

Mike Cotton

A parametric equation in the plane is a pair of functions   where the two continuous functions define an ordered pair (x,y). The two equations are usually called the parametric equations of a curve. The extent of the curve will depend on the range of t.

Part I

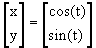Let's take a look at the parametric equation , with the interval 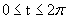. The graph of this equation can be seen in Figure 1 below.



This graph was created by Graphing Calculator 3.2.

Figure 1

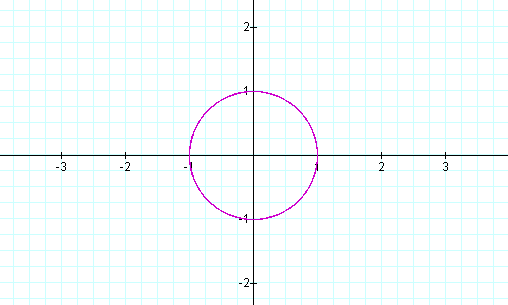
Keep in mind that the curve above is over the interval . That is, if the interval was 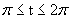then only the bottom half of the circle would be the curve. See Figure 2 below.


This graph was created by Graphing Calculator 3.2.

Figure 2

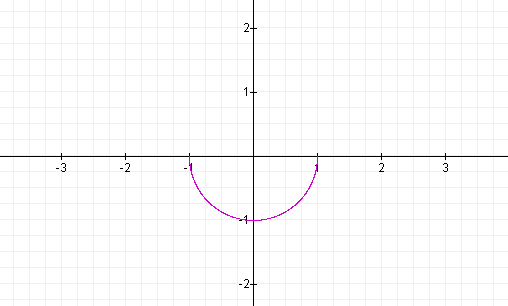
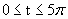If the interval is , then the curve would start at (1,0) and create 2½ revolutions and end at (-1,0). The list below shows the values of x and y that correspond to multiples of  π/4 for the parameter t.
t x = cos t y = sin t
0 1 0
π/4 1/√2 1/√2
π/2 0 1
3π/4 -1/√2 1/√2
π -1 0
5π/4 -1/√2 -1/√2
3π/2 0 -1
7π/4 1/√2 -1/√2
2π 1 0
9π/4 1/√2 1/√2
5π/2 0 1
11π/4 -1/√2 1/√2
3π -1 0
13π/4 -1/√2 -1/√2
7π/2 0 -1
15π/4 1/√2 -1/√2
4π 1 0
17π/4 1/√2 1/√2
9π/4 0 1
19π/4 -1/√2 1/√2
5π -1 0

Part II

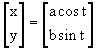Let's take a look at the parametric equation , with the interval 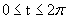. Let b = 1, and let a vary.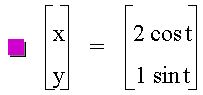





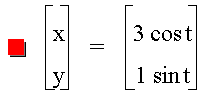
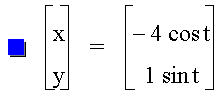
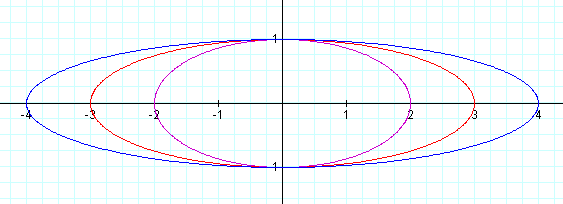
This graph was created by Graphing Calculator 3.2.
Figure 3

Since a doesn't equal b the result is an ellipse. The list below shows the values of x and y that correspond to multiples of  π/4 for the parameter t.
t x = cos t x = 2cos t x = 3cos t x = -4cos t y = sin t
0 1 2 3 -4 0
π/4 1/√2 2/√2 3/√2 -4/√2 1/√2
π/2 0 0 0 0 1
3π/4 -1/√2 -2/√2 -3/√2 4/√2 1/√2
π -1 -2 -3 4 0
5π/4 -1/√2 -2/√2 -3/√2 4/√2 -1/√2
3π/2 0 0 0 0 -1
7π/4 1/√2 2/√2 3/√2 -4/√2 -1/√2
2π 1 1 3 -4 0


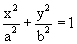What is interesting to note is that for a = 2 & 3 the curve starts at (1,0) and goes counter clock-wise, where the curve for a = -4 starts at (-4,0) and proceeds clock-wise. Also, the equation of an ellipse is  .  Multiplying the equation by a2b2 we get the equation 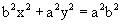.  If a = b then we get the equation x2 +y2 = a2 which is the equation for the circle.
Part III

Let's take another look at the parametric equation , with the interval . This time let a = 1, and let b vary.

  
This graph was created by Graphing Calculator 3.2.
Figure 4

Again, since a doesn't equal b the result is an ellipse. The list below shows the values of x and y that correspond to multiples of  π/4 for the parameter t.
t x = cos t y = sin t y = 2sin t y = -3sin t y = 4sin t
0 1 0 0 0 0
π/4 1/√2 1/√2 2/√2 -3/√2 4/√2
π/2 0 1 2 -3 4
3π/4 -1/√2 1/√2 2/√2 -3/√2 4/√2
π -1 0 0 0 0
5π/4 -1/√2 -1/√2 -2/√2 3/√2 -4/√2
3π/2 0 -1 -2 3 -4
7π/4 1/√2 -1/√2 -2/√2 3/√2 -4/√2
2π 1 0 0 0 0

What is interesting to note is that for b = 2 & 4 the curve starts at (1,0) and goes counter clock-wise, where the curve for b = -3 also starts at (1,0) but proceeds clock-wise.

Assignment 9        Return to main Page        Assignment 11