
Assignment 4: Centers of a Triangle
by
Mike Cotton
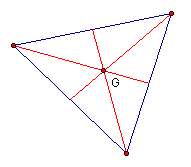
The CENTROID (G) of a triangle is the common
intersection of the three medians. A median of a triangle is the
segment from a vertex to the midpoint of the opposite side.
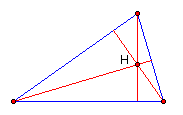
The ORTHOCENTER (H) of a triangle is the common intersection of the
three lines containing the altitudes. An altitude is a perpendicular
segment from a vertex to the line of the opposite side. (Note: The foot
of the perpendicular may be on the extension of the side of the
triangle.)
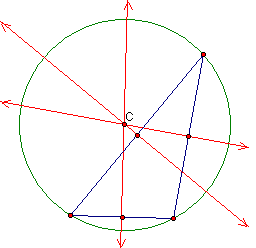
The CIRCUMCENTER (C) of a triangle is the point in the
plane equidistant from the three vertices of the triangle.
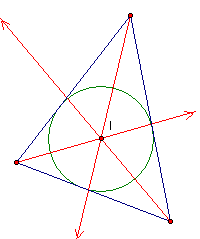
The INCENTER (I) of a triangle is the point on the interior of the
triangle that is equidistant from the three sides.
After performing several investigations it was found that if the
triangle is positioned such that one side is fixed horizontally
(segment YZ), and
the vertex that is not on the horozontal side (vertex X) is moved
horizontally
(on line Base,either above of below the fixed side) the orthocenter
traces a
parabola. See the figure below.
Figure1
What is interesting about this figure is that the distance from the
focus to the directrix (FocusM = 1.000 in.) for the parabola is half
the lnegth of the
segment ZX
(XZ = 2.00 in.) when the vertex Z is a right angle. That is,
there is a right triangle with the right angle at Z. The distance from
Z to
X' represents length of segment ZX when there is a right angle at
vertex Z. The example above is where segment ZX is less than half of
segment YZ.
Below are examples, one where segment ZX = 1/2 segment YZ (Figure 2),
and the other is where segment ZX is greater then one-half the length
of segment YZ (Figure 3).
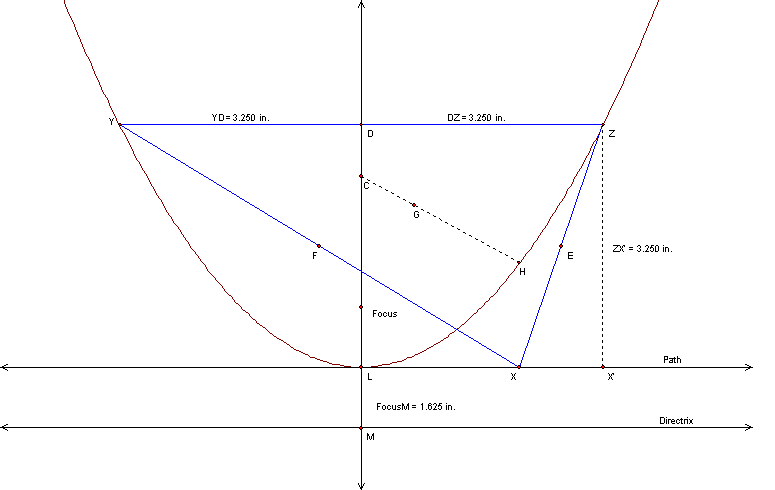
Figure 2
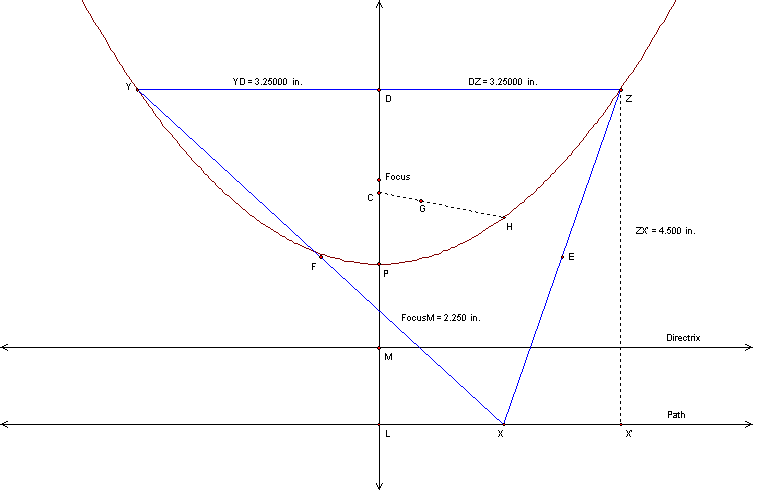
Figure 3
Assignment 3
Return to main Page
Assignment 5






