Assignment 6: Explorations with GSP
by
Mike Cotton
For this assignment the following problen needs to be
solved.
A 4 by 4 picture hangs on a wall such that its bottom edge is 2 ft
above your eye level. How far back from the picture should you stand,
directly in front of the picture, in order to view the picture under
the maximum angle? (Note: I used inches instead of feet, but the
solution for the maximum angle will be the same value as if I used
feet.)
Figure 1
The maximum angle is 30º.
The solution for this problem is shown below
in Figure 2. When the length of the segment a, segment b, and segment c
are all the same length then the angle is a maximum. Note that point M
is the orthocenter of the triangle TEB. There are also three isosceles
triangles. The first one is triangle TME, the next one is triangle TMB,
and the third one is triangle BME. If you would like to change the
height of the picture or the distance the eye level is from the middle
of the picture, just click on the picture below. (Note: For some reason
the units on the drawing are 96 times the units on this page. I'll try
to figure it out.)
Figure 2
There are at least two different ways to graphically
solve for the maximum angle. Please see the following.
One way to solve for the maximum angle is to create
circles with centers at T & B, and with radius equal to the
distance between points P & L. Next move point E until points A
& M coincide. Click on the figure to move some of the points.

Figure 3
A second way to solve for the maximum angle is to create
perpendicular bisectors through the midpoints of segment 1 and segment
2. The intersection of these two lines (point M) will be along the
horizontal line that runs throught
the middle of the picture. Next Move point E until points A & M
coincide. Click on the figure to move some of the points.
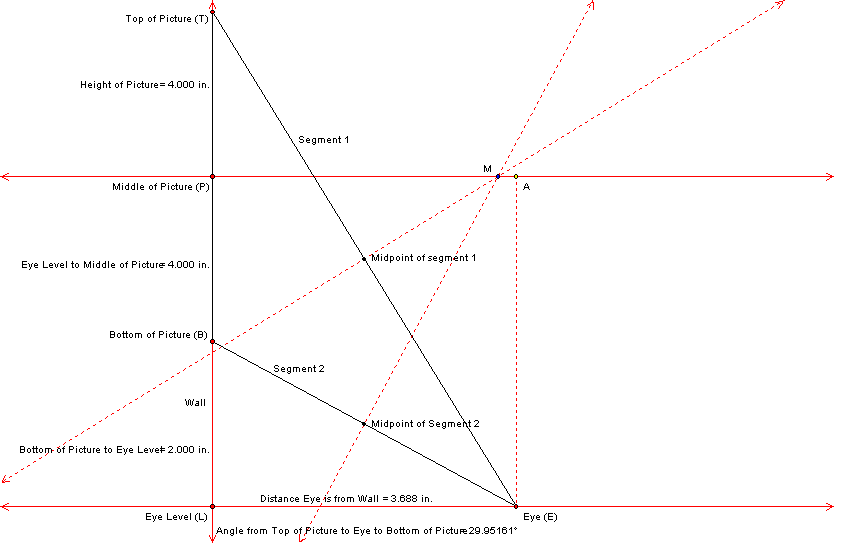
Figure 4
Assignment 5
Return to main Page
Assignment 7