Assignment 7: Tangent Circles

by

Mike Cotton

The problem for this assignment is as follows:  Given two circles and a point on one of the circles. Construct a circle tangent to the two circles with one point of tangency being the designated point.
  Below is a figure that represents the problem statment. One of the circles is green with center G, and the other circle is blue and has center Bl. Point T is the desired point of tangency on the green circle.


Figure 1

There are two different tangent circles that will solve the problem. One solution is for the tangent circle to be inside the green circle, and to have the red circle outside of it (Figure 2). The second solution is for the tangent circle to again be inside the green circle, and to have the red circle inside of it (Figure 3)

.                               
Figure 2                                                                                         Figure 3

Click on each figure above to manipulate the geometry.
The method of construction is similar for both solutions.  1. Construct a line (red) through points G & T (As you can see from above the center (Bk) of the tangent circle is between G & T).  2. Construct a circle with center T and same radius as the blue circle (dashed blue circle).  3. This step is the difference in the two solutions. For solution shown in Figure 2 create a point (C) at the intersection of the (red) line and the new circle at the point outside the green circle. For solution shown in Figure 3 create a point (C) at the intersection of the (red) line and the new circle at the point inside the green circle.  4. This step and the ones that follow are for both solutions. Construct a segment between points C & Bl.  5. Next, construct a perpendicular line (purple) throught the line created in the previous step.  6.The point where the (purple) line intersects the (red) line is the center of the (black) tangent circle.

                            
Figure 4                                                                                                Figure 5
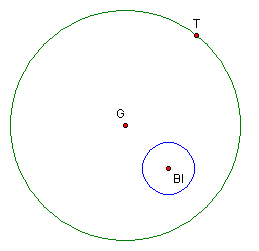
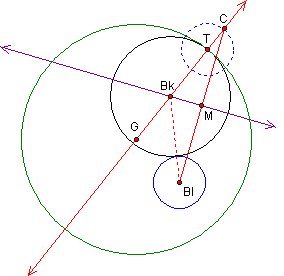
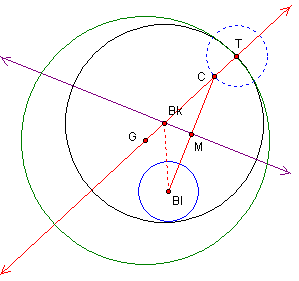
As the point T is moved along the circumference of the green circle, the center (Bk) of the tangent circle will trace an ellipse or a hyperbola. Click here to experiment with tracing.  Note: The two circles (green & blue) can be moved and resized by manipulating their centers.

Assignment 6        Return to main Page        Assignment 8