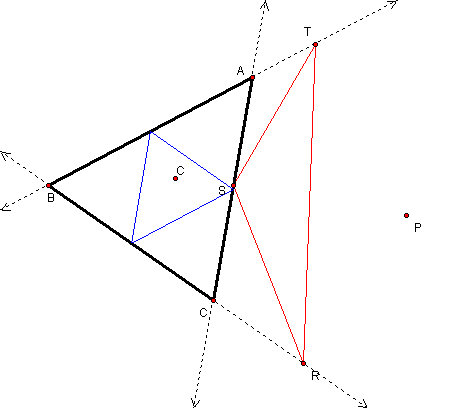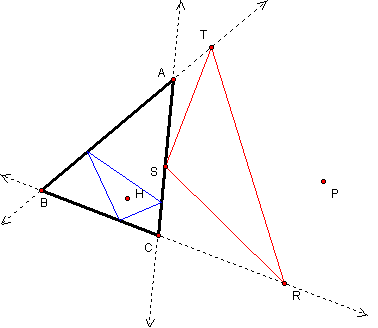
Figure 2
The figure above (Figure 2) shows
triangle ABC with its orthic triangle within (blue). Click on the image
to move point P so it coincides with point H (orthocenter of triangle
ABC). The pedal triangle will coincide with the orthic triangle when
the pedal point P coincides with point H. This is true even if triangle
ABC is obtuse.