The
Department of Mathematics Education
William Daly
EMAT6680
Write Up #1
Summer 03
The Ubiquitous Sine Function
The familiar sine function is pervasive in virtually every discipline of science and engineering. Any physical behavior that is characterized by periodicity is described by some variant of the sine function, whether it is mechanical vibrations , musical notes or resonating cavities. The simplest general form of the sine function is y=a sin( bx +c).
This article explores the physical meaning of the variables and parameters of this general expression. This exploration will be done relative to this function as a description of musical notes, although other disciplines typically have similar analogs to parameters associated with musical notes as sound waves. The opening discussion covers the basic parameters of this equation as they relate to loudness and tone. This is followed by a discussion of how variations of this equation combine to create a description of the more complicated characteristic of sound called timbre.
In the context of musical notes, the independent variable x represents time in seconds, although more traditionally the variable t would be used. The dependent variable is y, which is the value of the air pressure impinging on the eardrum at each instant of time. The remaining parameters are a,b and c.
Let us select the parameter b first to observe. To do so, fix a and c. Notice that something other than zero must be selected for a so that y ≠ 0. However c=0 provides an acceptable initial parameter. So now the expression becomes y=sin(bx)as shown in Figure 1.
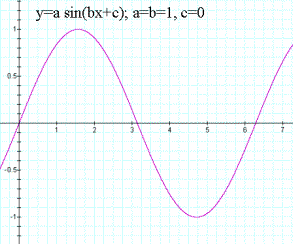
Figure 1: Sine function graph.
Notice in this figure that the x axis crossing is at nπ for all integers, or 2nπ for each full cycle. Consider how one can describe a graph of the sine function that crosses the x axis with a frequency of once every second. To do so simply involves replacing n with a variable for frequency. So now the variable b can be defined as b=2πf. The unit of measure of f is Hertz, abbreviated Hz (cycles/second). So the graph of the sine function for f=1Hz is shown in Figure 2.
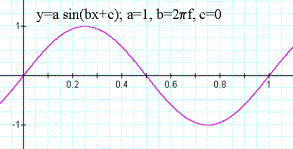
Figure 2: Sine function graph with frequency of 1 Hz.
Next consider the effect of variations in the variable f (which of course varies b, as b=2πf). To see the effect of changing f, select values corresponding to the two musical notes A in the fourth and fifth octaves of the musical scale. See Figure 3 for the effect of this variation. Notice several features of this graph. First, both graphs go through the point (0,0); this will become important later when we discuss the impact of the parameter c. The two values of A correspond to frequencies of 440Hz in the fourth octave and 880Hz in the fifth octave. As expected, since the fifth octave A is twice the frequency of the fourth octave, there are exactly two cycles of the fifth octave A within the fourth octave A. How is the frequency parameter related to the x axis crossings? Notice that zero crossings for a full cycle are at 0.002272 and 0.001136 seconds for the fourth and fifth octaves, respectively. These values are called the period, T, of the sine function and is the reciprocal of the frequencies. That is T1= 0.002272 sec. = 1 / 440Hz and T2 = 0.001136 sec. = 1 / 880Hz. The frequency represents the pitch of the musical note.
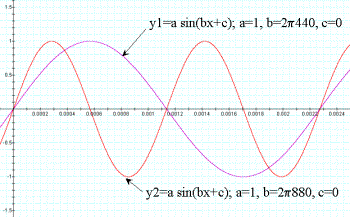
Figure 3: Graph of note A, octaves 4 and 5, only varying b.
Now that the parameter b (related to frequency or pitch) is understood, consider next the parameter, a. Figure 3 is re-plotted Figure 4. This plot is an animation as a is varied from 0 to 1.25. Notice in the animation that as a varies, there is no effect whatsoever on the zero crossings. Therefore the frequency, or pitch, is unaffected by the value of a. Also, all graphs still go through (0,0). Notice that the maximum and minimum values of y vary directly with a. The physical interpretation of this is that the maximum pressure of the sound wave is directly related to a, which is also known variably as amplitude, intensity or loudness of the musical note.
Having seen that pitch and loudness are affected by a and b, what is the effect of c? Setting a=1, and b1=440Hz and b2=880Hz, view Figure 5 to see the effect as c is varied from 0 to π/2. Notice that a variation of c effect neither the amplitude of y (maximum and minimum are unchanged) nor the pitch (the spacing of the zero crossings is unchanged). The only effect of changing c is to delay or advance the sine waves. To the human ear this has no effect on what is heard, so what is the point of considering c?
A sine wave is a pure tone. There are no musical instruments that create a pure sine wave, even though the frequency may be the same. One of the characteristics of musical instruments that distinguish them from others is timbre, which is lends importance to the parameter c. Before considering the parameter c, we must first see how to mathematically describe tones other than a pure sine wave. This was first proposed by Fourier at the turn of the 19th century. Fourier proposed that any periodic waveform, regardless of shape, can be expressed as a summation of a series of sines and cosines (which is just a sine shifted by c=π/2). To see a simple example of this, refer to Figure 6, which shows three waveforms at the same frequency as the fourth octave A.
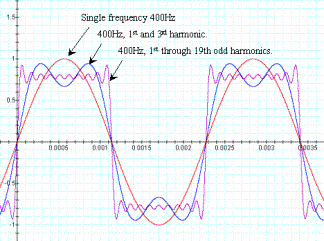
Figure 6: Fourth Octave A; fundamental, 3rd overtone, and 3rd through 19th overtones.
The pure sinewave, or the fundamental, is shown in red. A summation of the fundamental and the third harmonic is show in blue. In violet, a summation of all harmonics out to the 19th harmonic is shown. Note that each of the harmonics are weighted as follows:
![]()
Weighted in this way, notice that the resultant summation is approaching a square wave of exactly the same frequency of the fundamental. In fact, if N is allowed to approach infinity, as suggested by the graph, the result approaches a square wave. The only qualifier to this is that a spike occurs at the discontinuity of the perfect square as a result of this infinite sum. This is know as Gibbs phenomenon. This is an artifact of the discontinuity, which is beyond the scope of this paper. Suffice it to say that any periodic function may be reconstructed of an infinite series if sines and cosines as shown above.
So what does all of this have to do with the parameter c? Recall that the summation of a pure sine wave and its harmonics cited above changes a musical notes timbre by changing the tone from a pure sine wave to a square wave (or whatever periodic function we choose by judicious selection of the amplitudes and overtones). The result showing the 3rd through 19th harmonics restated in Figure 7, animated with various values of c in each of the terms of the summation. Note that for each of these sine waves, the amplitude a is not changed, nor is the frequency, related to b. Only the delay term, or phase, is changed. While for the pure sine wave changing c does not affect the basic shape, doing so for a composite of sines has a profound effect on the wave shape, or timbre.
To conclude, the parameters a,b andc in y=a sin (bx+c) represent physical parameters associated with a multitude of phenomena in widely varying disciplines. These parameters are independent of one another in the features of the sinewave that are affected.. The parameter a is the intensity, amplitude, or in acoustic terms, the loudness. Parameter b is the frequency, or the number of vibration or periods per second. And finally c is known as the phase of the signal. Although delay in a waveform is important, its effect is most dramatic when considering periodic function comprised of a summation of sines and cosines. In terms of musical notes, the resonant cavity of unique instruments imparts a different amplitude and phase to the harmonic content, which give the instrument its unique timbre as illustrated in Figure 7. Note that the above summation of sines is only one of an infinite possible choices, in which both the b and c terms may be varied.
